ДИСПЕРСИОННЫЙ АНАЛИЗ

Общие положения

Дисперсионный анализ предназначен для сравнения нескольких средних значений или для выявления степени влияния различных факторов на выходные параметры. Иначе говоря, это анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов. Заключения относительно математических ожиданий, оценками которых по экспериментальным данным являются средние арифметические значения параметров, делаются с помощью сравнения выборочных дисперсий, вычисленных двумя различными методами.

Задача дисперсионного анализа состоит в том, чтобы из общей вариативности признака вычленить:
* изменчивость, обусловленную действием каждой из исследуемых независимых переменных;
* изменчивость, обусловленную взаимодействием исследуемых признаков;
* случайную изменчивость, обусловленную всеми другими неизвестными переменными.

Если имеем дело с многофакторным процессом, то с помощью дисперсионного анализа удается определить дисперсии, обусловленные действием каждого фактора в отдельности, и оценить статистическую значимость этих величин.

Используемые в дисперсионном анализе критерии значимости основаны на предположении о том, что распределение вероятностей является нормальным или же другим стандартным распределением, связанным с нормальным (?2, t-распределение, F ? Фишера).

Однофакторный дисперсионный анализ в системе Statistica

Рассмотрим пример проверки гипотезы на уровне значимости 0,05 о том, что водонасыщение образцов грунта, взятого с разных экспериментальных полигонов (табл.), различно. С каждого полигона было взято по 10 образцов. Задача состоит в проверке гипотезы H0 о равенстве математических ожиданий случайных величин ?водонасыщения образцов грунта, взятого с трёх экспериментальных полигонов.

Таблица
Результаты измерений водонасыщения образцов грунта

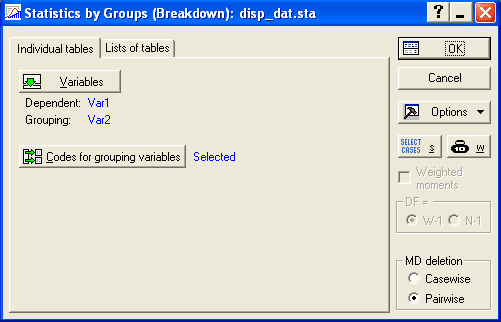
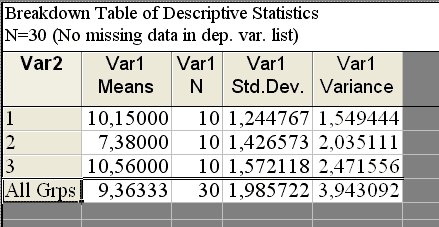
Создадим таблицу с двумя столбцами 30 строками. В Var 1 занесём данные по водонасыщению образцов из табл. 9.2, в Var 2 – обозначения групп, определяющих номер полигона – 1 (первые 10 строк), 2 (строки 11–20), 3 (строки 21–30).

Схема дисперсионного анализа применима и в тех случаях, когда градации фактора отличаются лишь качественно, например, цвет окраски, музыкальный жанр; разные формы заболевания, разные экспериментаторы и т.д.

Расчёты выполняются в модуле Statistics/ Basic Statistics and Tables/ Breakdown and one-way ANOVA (однофакторный дисперсионный анализ).
В окне выбора переменных (рис. 9.1) нажатием кнопки Variables выбираем Var 1 как зависимую переменную (Dependent Variables:), Var 2 как группирующую переменную (Grouping Variables:), ОК.

В окне результатов (рис. 9.2) во вкладке Descriptives отметим следующие статистики: Valid N (количество наблюдений), Standard deviations (стандартные отклонения) и Variances (дисперсии).

Нажав кнопку Summary, получим таблицу результатов (рис. 9.3).

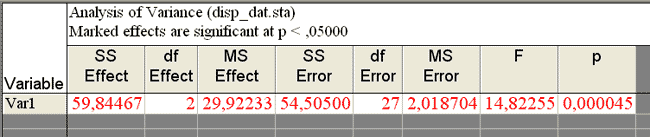
Возвратимся в предыдущее окно. Перейдя к вкладке ANOVA & tests, выполним дисперсионный анализ, нажав кнопку Analysis of Variance (дисперсионный анализ). В таблице дисперсионного анализа приводятся:
* SS Effect = 59,84467 – сумма квадратов отклонений выборочных средних групп от общего среднего между группами SSA;
* df Effect = 2 – число степеней свободы для SS Effect;
* MS Effect = 29,92233 – среднее значение суммы квадратов S2A;
* SS Error = 54,50500 – сумма квадратов отклонений результатов наблюдений от выборочных средних групп внутри групп SS0;
* df Error = 27 – число степеней свободы для SS Error;
* MS Error = 2,018704 – среднее значение суммы квадратов S20;
* F = 14,82255 – выборочное значение F-статистики;
* р = 0,000045 – вычисленный уровень значимости.

Метод дисперсионного анализа позволяет определить, что перевешивает ? вариативность признака внутри групп или между группами

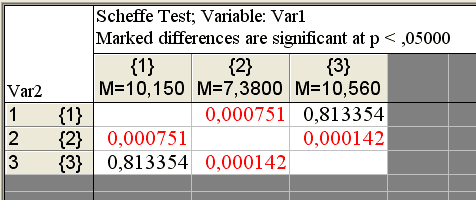
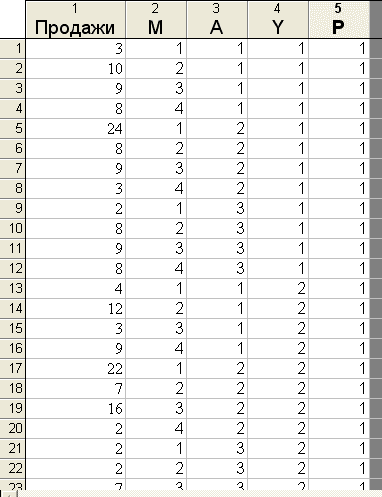
Так как вычисленный уровень значимости р меньше заданного уровня значимости 0,05, то гипотеза о равенстве средних отвергается. Таким образом, водонасыщение образцов грунта, взятых с разных полигонов, различно.
Определим, какой полигон дал различие в водонасыщении. Для ответа на этот вопрос возвращаемся в окно (рис. 9.2) и выполняем Post-hoc comparisons of means (сравнение средних) по методу Шеффе (Sheffe test).
В таблице попарного сравнения средних (рис. 9.5) указаны уровни значимости для проверки гипотез о равенстве средних для всех пар. Гипотеза о том, что математическое ожидание первой группы равно математическому ожиданию третьей группы принимается на уровне значимости р=0,813354, остальные гипотезы о равенстве математических ожиданий отклоняются. Аналогичный результат даёт другой способ сравнения средних (кнопка LSD test or planned comparison).

Проверка предположений дисперсионного анализа

Напомним, что при применении дисперсионного анализа предполагается, что исходные данные – независимые выборки наблюдений, полученные из нормально распределённых генеральных совокупностей, имеющих одну и ту же дисперсию. выполнение этих предположений можно проверить в пакете Statistica. Один из способов проверки нормальности состоит в том, что исходные данные по группам наносятся на нормальный вероятностный график. Для этого в окне результатов во вкладке ANOVA & tests нужно нажать кнопку Categorized normal prob. plots (категоризованные нормальные вероятностные графики). Для наших данных получим следующие графики.

Точки, соответствующие нормально распределённым данным, укладываются на прямые. Как показывают графики, исходные данные достаточно плотно группируются относительно прямых.
Для проверки выполнения предположения о равенстве дисперсий по группам используются так называемые критерии однородности дисперсий (Test of Homog. of Variances). В пакете Statistica для этих целей можно использовать критерий Левена (Levene test....) либо критерий Брауна-Форсайта (Brown-Forsythe Test...).
Чтобы выполнить эти процедуры нужно нажать соответствующие кнопки в окне результатов дисперсионного анализа (рис. 9.2, вкладка ANOVA & tests). Для исходных данных нашего примера гипотеза о равенстве дисперсий по группам принимается по этим двум критериям на уровнях значимости р=0,8017 и р=0,8035 соответственно.

Многофакторный дисперсионный анализ

Многофакторный дисперсионный анализ рассмотрим на следующем примере. Четыре группы продавцов продавали штучный товар. Каждая группа была подготовлена по определённой методике (фактор M=1, 2, 3, 4). Товар рекламировался по телевидению, в газете и по радио (фактор A=1, 2, 3). Кроме того, он был расфасован в различные упаковки (фактор Y=1, 2, 3). Эксперимент повторялся дважды (P=1, 2). После окончания двух сроков были получены следующие результаты по количеству продаж

Таблица
Результаты продаж

Фрагмент таблицы с исходными данными приведен на рис. 9.7.

Для расчётов необходимо выполнить команду Statistics/ ANOVA/ Main effects ANOVA. По нажатию кнопки Variables определите переменные: Dependent variable list – Продажи, Categorical predictors (factors) – все остальные, и нажмите ОК. Теперь достаточно нажать кнопку All effects, и на экране появятся результаты общего дисперсионного анализа. Если эти результаты выделены красным цветом, – фактор оказывает существенное влияние. Более строго, анализируя критерий Фишера или значение р, можно сказать, что на количество продаж существенное влияние оказывают факторы M (методика обучения) и A (реклама).

Результаты

Примеры, рассмотренные в этой главе, демонстрируют технику вычислений в системе Statistica. Применение дисперсионного анализа, как и большинства других статистических методов для получения обоснованных и практически важных выводов требует значительно больше исходных данных. Только в этом случае можно говорить о проверке нормальности и других предположений. Вопрос о том, насколько оправдано применение параметрических статистических методов, является достаточно сложным. В связи с этим, в тех случаях, когда выполнение предположений дисперсионного анализа проблематично, следует использовать также и соответствующие непараметрические процедуры и сравнить результаты.

Вообще F-критерий очень устойчив к отклонению от нормальности. Если эксцесс больше нуля, то значение F-статистики может стать очень маленьким. Нулевая гипотеза при этом не может быть отвергнута, хотя она и не верна. Ситуация меняется на противоположную, если эксцесс меньше нуля. Асимметрия распределения обычно незначительно влияет на F-статистику. Если число наблюдений в ячейке достаточно большое, то отклонение от нормальности не имеет особого значения в силу центральной предельной теоремы, в соответствии с которой распределение среднего значения при большом объёме выборки близко к нормальному независимо от начального распределения.