ФАКТОРНЫЙ АНАЛИЗ

Идея факторного анализа

При исследовании сложных объектов, явлений, систем факторы, определяющие свойства этих объектов, очень часто невозможно измерить непосредственно, а иногда неизвестно даже их число и смысл. Но для измерения могут быть доступны другие величины, так или иначе зависящие от интересующих нас факторов. Причем, когда влияние неизвестного интересующего нас фактора проявляется в нескольких измеряемых признаках или свойствах объекта, эти признаки могут обнаруживать тесную связь между собой и общее число факторов может быть гораздо меньше, чем число измеряемых переменных.

Для выявления факторов, определяющих измеряемые признаки объектов, используются методы факторного анализа

В качестве примера применения факторного анализа можно указать изучение свойств личности на основе психологических тестов. Свойства личности не поддаются прямому измерению. О них можно судить только по поведению человека или характеру ответов на вопросы. Для объяснения результатов опытов их подвергают факторному анализу, который и позволяет выявить те личностные свойства, которые оказывают влияние на поведение индивидуума.
В основе различных методов факторного анализа лежит следующая гипотеза: наблюдаемые или измеряемые параметры являются лишь косвенными характеристиками изучаемого объекта, в действительности существуют внутренние (скрытые, латентные, не наблюдаемые непосредственно) параметры и свойства, число которых мало и которые определяют значения наблюдаемых параметров. Эти внутренние параметры принято называть факторами.

Цель факторного анализа – сконцентрировать исходную информацию, выражая большое число рассматриваемых признаков через меньшее число более ёмких внутренних характеристик явления, которые, однако, не поддаются непосредственному измерению

Установлено, что выделение и последующее наблюдение за уровнем общих факторов даёт возможность обнаруживать предотказные состояния объекта на очень ранних стадиях развития дефекта. Факторный анализ позволяет отслеживать стабильность корреляционных связей между отдельными параметрами. Именно корреляционные связи между параметрами, а также между параметрами и общими факторами содержат основную диагностическую информацию о процессах. Применение инструментария пакета Statistica при выполнении факторного анализа исключает необходимость использования дополнительных вычислительных средств и делает анализ наглядным и понятным для пользователя.

Результаты факторного анализа будут успешными, если удается дать интерпретацию выявленных факторов, исходя из смысла показателей, характеризующих эти факторы. Данная стадия работы весьма ответственная; она требует чёткого представления о содержательном смысле показателей, которые привлечены для анализа и на основе которых выделены факторы. Поэтому при предварительном тщательном отборе показателей для факторного анализа следует руководствоваться их смыслом, а не стремлением к включению в анализ как можно большего их числа.

Сущность факторного анализа

Приведём несколько основных положений факторного анализа. Пусть для матрицы Х[1:p, 1:n] измеренных параметров объекта существует ковариационная (корреляционная) матрица C[1:р, 1:p], где р – число параметров, n – число наблюдений. Путем линейного преобразования X=QY+U можно уменьшить размерность исходного факторного пространства Х[1:р] до уровня Y[1:p'], при этом р'<<р. Это соответствует преобразованию точки, характеризующей состояние объекта в j-мерном пространстве, в новое пространство измерений с меньшей размерностью р'. Очевидно, что геометрическая близость двух или множества точек в новом факторном пространстве означает стабильность состояния объекта.

Матрица Y[1:р';1:n] содержит ненаблюдаемые факторы, которые по существу являются гиперпараметрами, характеризующими наиболее общие свойства анализируемого объекта. Общие факторы чаще всего выбирают статистически независимыми, что облегчает их физическую интерпретацию. Вектор наблюдаемых признаков Х[1:р] имеет смысл следствия изменения этих гиперпараметров.

Матрица U[1:р', 1:n] состоит из остаточных факторов, которые включают в основном ошибки измерения признаков x(i). Прямоугольная матрица Q[l:р, 1:р'] содержит факторные нагрузки, определяющие линейную связь между признаками и гиперпараметрами.
Факторные нагрузки – это значения коэффициентов корреляции каждого из исходных признаков с каждым из выявленных факторов. Чем теснее связь данного признака с рассматриваемым фактором, тем выше значение факторной нагрузки. Положительный знак факторной нагрузки указывает на прямую (а отрицательный знак – на обратную) связь данного признака с фактором.

Таким образом, данные о факторных нагрузках позволяют сформулировать выводы о наборе исходных признаков, отражающих тот или иной фактор, и об относительном весе отдельного признака в структуре каждого фактора.

Модель факторного анализа похожа на модели многомерного регрессионного и дисперсионного анализа. Принципиальное отличие модели факторного анализа в том, что вектор Y[1:p'] – это ненаблюдаемые факторы, а в регрессионном анализе – это регистрируемые параметры. В правой части уравнения (8.1) неизвестными являются матрица факторных нагрузок Q[1:р, 1:р'] и матрица значений общих факторов Y[1:р'].

Для нахождения матрицы факторных нагрузок используют уравнениеQQ_т=S–V, где Q_т – транспонированная матрица Q, V – матрица ковариаций остаточных факторов U[1:p?], т.е. . Уравнение решается путем итераций при задании некоторого нулевого приближения ковариационной матрицы V(0). После нахождения матрицы факторных нагрузок Q[1:р, 1:р'] вычисляются общие факторы (гиперпараметры) по уравнению
Y[1:n]=(Q_тV_-1)Q_-1Q_тV_-1X[1:n]

Пакет статистического анализа Statistica позволяет в диалоговом режиме вычислить матрицу факторных нагрузок, а также значения нескольких заранее заданных главных факторов, чаще всего двух – по первым двум главным компонентам исходной матрицы параметров.

Факторный анализ в системе Statistica

Рассмотрим последовательность выполнения факторного анализа на примере обработки результатов анкетного опроса работников предприятия. Требуется выявить основные факторы, которые определяют качество трудовой жизни.

На первом этапе необходимо отобрать переменные для проведения факторного анализа. Используя корреляционный анализ, исследователь пытается выявить взаимосвязь исследуемых признаков, что, в свою очередь, даёт ему возможность выделить полный и безызбыточный набор признаков путём объединения сильно коррелирующих признаков.

Если проводить факторный анализ по всем переменным, то результаты могут получиться не совсем объективными, так как некоторые переменные определяется другими данными, и не могут регулироваться сотрудниками рассматриваемой организации.

Для того чтобы понять, какие показатели следует исключить, построим по имеющимся данным матрицу коэффициентов корреляции в Statistica: Statistics/ Basic Statistics/ Correlation Matrices/ Ok. В стартовом окне этой процедуры Product-Moment and Partial Correlations (рис. 4.3) для расчёта квадратной матрицы используется кнопка One variable list. Выбираем все переменные (select all), Ok, Summary. Получаем корреляционную матрицу.

Если коэффициент корреляции изменяется в пределах от 0,7 до 1, то это означает сильную корреляцию показателей. В этом случае можно исключить одну переменную с сильной корреляцией. И наоборот, если коэффициент корреляции мал, можно исключить переменную из-за того, что она ничего не добавит к общей сумме. В нашем случае сильной корреляции между какими-либо переменными не наблюдается, и факторный анализ будем проводить для полного набора переменных.

Для запуска факторного анализа необходимо вызвать модуль Statistics/ Multivariate Exploratory Techniques (многомерные исследовательские методы)/ Factor Analysis (факторный анализ). На экране появится окно модуля Factor Analysis.

Для анализа выбираем все переменные электронной таблицы; Variables (переменные): select all, Ok. В строке Input file (тип файла входных данных) указывается Raw Data (исходные данные). В модуле возможны два типа исходных данных – Raw Data (исходные данные) и Correlation Matrix – корреляционная матрица.

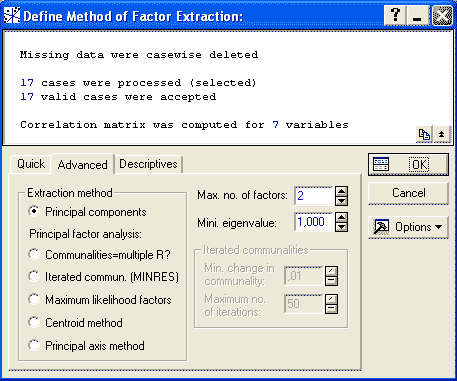
В разделе MD deletion задаётся способ обработки пропущенных значений:
* Casewise – способ исключения пропущенных значений (по умолчанию);
* Pairwise – парный способ исключения пропущенных значений;
* Mean substitution – подстановка среднего вместо пропущенных значений.
Способ Casewise состоит в том, что в электронной таблице, содержащей данные, игнорируются все строки, в которых имеется хотя бы одно пропущенное значение. Это относится ко всем переменным. В способе Pairwise игнорируются пропущенные значения не для всех переменных, а лишь для выбранной пары.

Выберем способ обработки пропущенных значений Casewise.

Statistica обработает пропущенные значения тем способом, который указан, вычислит корреляционную матрицу и предложит на выбор несколько методов факторного анализа.

Верхняя часть окна является информационной. Здесь сообщается, что пропущенные значения обработаны методом Casewise. Обработано 17 наблюдений и 17 наблюдений принято для дальнейших вычислений. Корреляционная матрица вычислена для 7 переменных. Нижняя часть окна содержит 3 вкладки: Quick, Advanced, Descriptives.

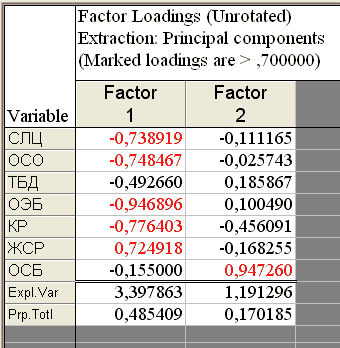
Во вкладке Descriptives (описательные статистики) имеются две кнопки:
1- просмотреть корреляции, средние и стандартные отклонения;
2- построить множественную регрессию.

Нажав на первую кнопку, можно посмотреть средние и стандартные отклонения, корреляции, ковариации, построить различные графики и гистограммы.

Во вкладке Advanced, в левой части, выберем метод (Extraction method) факторного анализа: Principal components (метод главных компонент). В правой части выбираем максимальное число факторов (2). Задаётся либо максимальное число факторов (Max no of factors), либо минимальное собственное значение: 1 (eigenvalue).

Нажимаем Ok, и Statistica быстро произвёдет вычисления. На экране появляется окно Factor Analysis Results (результаты факторного анализа). Как говорилось ранее, результаты факторного анализа выражаются набором факторных нагрузок. Поэтому далее будем работать с вкладкой Loadings.

Верхняя часть окна – информационная:
Number of variables (число анализируемых переменных): 7;
Method (метод выделения факторов): Principal components (главных компонент);
Log (10) determinant of correlation matrix (десятичный логарифм детерминанта корреляционной матрицы): –1,6248;
Number of factors extracted (число выделенных факторов): 2;
Eigenvalues (собственные значения): 3,39786 и 1,19130.
В нижней части окна находятся функциональные кнопки, позволяющие всесторонне просмотреть результаты анализа, числено и графически.
Factor rotation – вращение факторов, в данном выпадающем окне можно выбрать различные повороты осей. С помощью поворота системы координат можно получить множество решений, из которого необходимо выбрать интерпретируемое решение.

Существуют различные методы вращения координат пространства. Пакет Statistica предлагает восемь таких методов, представленных в модуле факторного анализа. Так, например, метод варимакс соответствует преобразованию координат: вращение, максимизирующее дисперсию. В методе варимакс получают упрощённое описание столбцов факторной матрицы, сводя все значения к 1 или 0. При этом рассматривается дисперсия квадратов нагрузок фактора. Факторная матрица, получаемая с помощью метода вращения варимакс, в большей степени инвариантна по отношению к выбору различных множеств переменных.

Вращение методом квартимакс ставит целью аналогичное упрощение только по отношению к строкам факторной матрицы. Эквимакс занимает промежуточное положение ? при вращении факторов по этому методу одновременно делается попытка упростить и столбцы, и строки. Рассмотренные методы вращения относятся к ортогональным вращениям, т.е. в результате получаются некоррелированные факторы. Методы прямого облимина и промакс вращения относятся к косоугольным вращениям, в результате которых получаются коррелированные между собой факторы. Термин ?normalized? в названиях методов указывает на то, что факторные нагрузки нормируются, то есть делятся на квадратный корень из соответствующей дисперсии.

Из всех предлагаемых методов, мы сначала посмотрим результат анализа без вращения системы координат – Unrotated. Если полученный результат окажется интерпретируемым и будет нас устраивать, то на этом можно остановиться. Если нет, можно вращать оси и посмотреть другие решения.

Щёлкаем по кнопке "Factor Loading" и смотрим факторные нагрузки численно.

Напомним, что факторные нагрузки – это значения коэффициентов корреляции каждой из переменных с каждым из выявленных факторов.

Значение факторной нагрузки, большее 0,7 показывает, что данный признак или переменная тесно связан с рассматриваемым фактором. Чем теснее связь данного признака с рассматриваемым фактором, тем выше значение факторной нагрузки. Положительный знак факторной нагрузки указывает на прямую (а отрицательный знак ? на обратную) связь данного признака с фактором.
Итак, из таблицы факторных нагрузок было выявлено два фактора. Первый определяет ОСБ – ощущение социального благополучия. Остальные переменные обусловлены вторым фактором.

В строке Expl. Var (рис. 8.5) приведена дисперсия, приходящаяся на тот или иной фактор. В строке Prp. Totl приведена доля дисперсии, приходящаяся на первый и второй фактор. Следовательно, на первый фактор приходится 48,5 % всей дисперсии, а на второй фактор – 17,0 % всей дисперсии, всё остальное приходится на другие неучтенные факторы. В итоге, два выявленных фактора объясняют 65,5 % всей дисперсии.

Посмотрим результат факторного анализа графически, нажав на кнопку Plot of loadings, 2D.

Максимальное число общих факторов может быть равно количеству собственных чисел матрицы параметров. Но с увеличением числа факторов существенно возрастают трудности их физической интерпретации.

Сначала можно отобрать только факторы, с собственными значениями, большими 1. По существу, это означает, что если фактор не выделяет дисперсию, эквивалентную, по крайней мере, дисперсии одной переменной, то он опускается. Этот критерий используется наиболее широко. В приведённом выше примере на основе этого критерия следует сохранить только 2 фактора (две главные компоненты).

Можно найти такое место на графике, где убывание собственных значений слева направо максимально замедляется. Предполагается, что справа от этой точки находится только "факториальная осыпь". В соответствии с этим критерием можно оставить в примере 2 или 3 фактора.
Из рис. видно, что третий фактор незначительно увеличивает долю общей дисперсии.

Рекомендации по применению факторного анализа

Факторный анализ параметров позволяет выявить на ранней стадии нарушение рабочего процесса (возникновение дефекта) в различных объектах, которое часто невозможно заметить путём непосредственного наблюдения за параметрами. Это объясняется тем, что нарушение корреляционных связей между параметрами возникает значительно раньше, чем изменение одного параметра. Такое искажение корреляционных связей позволяет своевременно обнаружить факторный анализ параметров. Для этого достаточно иметь массивы зарегистрированных параметров.

Можно дать общие рекомендации по использованию факторного анализа вне зависимости от предметной области.
* На каждый фактор должно приходиться не менее двух измеренных параметров.
* Число измерений параметров должно быть больше числа переменных.
* Количество факторов должно обосновываться, исходя из физической интерпретации процесса.
* Всегда следует добиваться того, чтобы количество факторов было намного меньше числа переменных.

Критерий Кайзера иногда сохраняет слишком много факторов, в то время как критерий каменистой осыпи иногда сохраняет слишком мало факторов. Однако оба критерия вполне хороши при нормальных условиях, когда имеется относительно небольшое число факторов и много переменных. На практике более важен вопрос о том, когда полученное решение может быть интерпретировано. Поэтому обычно исследуется несколько решений с большим или меньшим числом факторов, и затем выбирается одно наиболее осмысленное.

Пространство исходных признаков должно быть представлено в однородных шкалах измерения, т. к. это позволяет при вычислении использовать корреляционные матрицы. В противном случае возникает проблема "весов" различных параметров, что приводит к необходимости применения при вычислении ковариационных матриц. Отсюда может появиться дополнительная проблема повторяемости результатов факторного анализа при изменении количества признаков. Следует отметить, что указанная проблема просто решается в пакете Statistica путем перехода к стандартизированной форме представления параметров. При этом все параметры становятся равнозначными по степени их связи с процессами в объекте исследования.

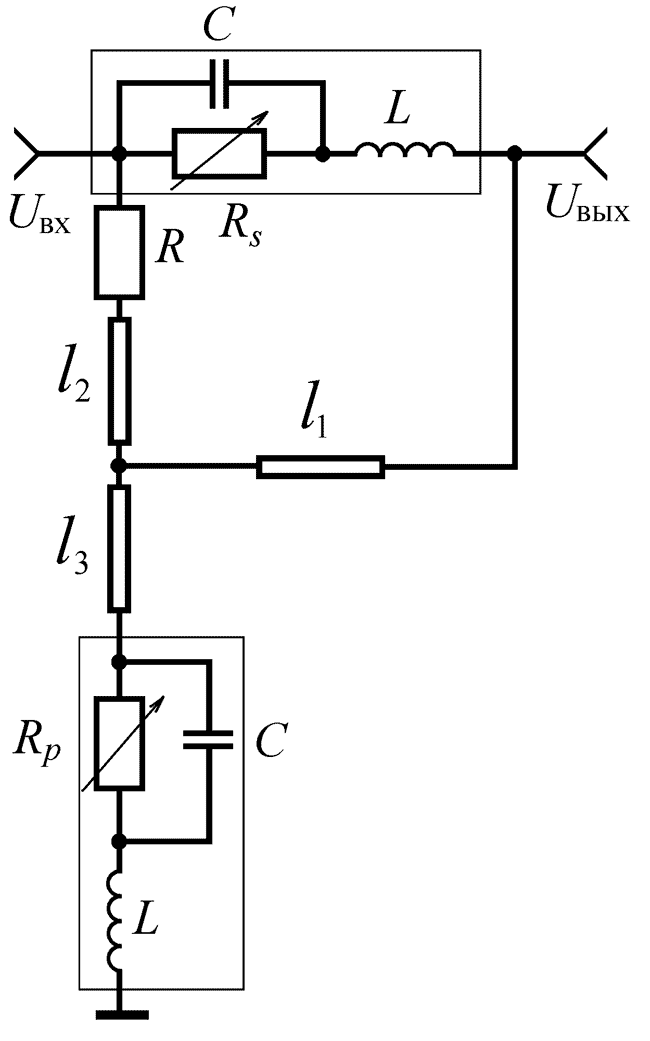
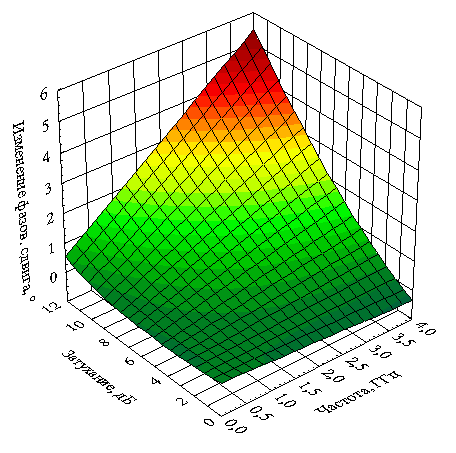
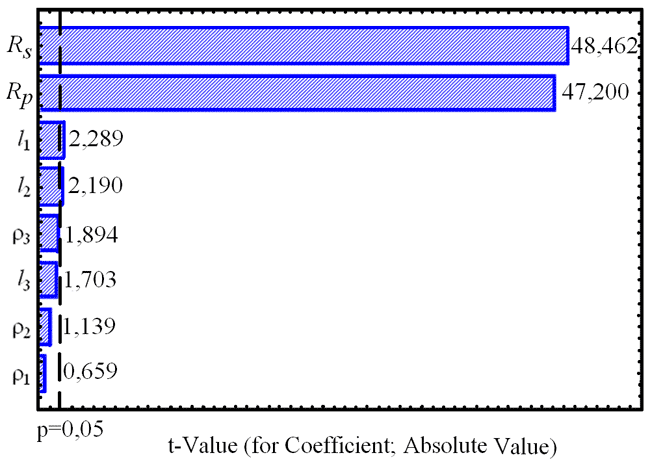
Если в наборе исходных данных имеются избыточные переменные и не проведено их исключение корреляционным анализом, то нельзя вычислить обратную матрицу (8.3). Например, если переменная является суммой двух других переменных, отобранных для этого анализа, то корреляционная матрица для такого набора переменных не может быть обращена, и факторный анализ принципиально не может быть выполнен. На практике это происходит, когда пытаются применить факторный анализ к множеству сильно зависимых переменных, что иногда случается, например, в обработке вопросников. Тогда можно искусственно понизить все корреляции в матрице путём добавления малой константы к диагональным элементам матрицы, и затем стандартизировать её. Эта процедура обычно приводит к матрице, которая может быть обращена, и поэтому к ней применим факторный анализ. Более того, эта процедура не влияет на набор факторов, но оценки оказываются менее точными.

Системой с переменными состояниями (СПС) называется система, отклик которой зависит не только от входного воздействия, но и от обобщенного постоянного во времени параметра, определяющего состояние. Регулируемый усилитель или аттенюатор ? это пример простейшей СПС, в котором коэффициент передачи может дискретно или плавно изменяться по какому-либо закону. Исследование СПС обычно проводится для линеаризованных моделей, в которых переходный процесс, связанный с изменением параметра состояния, считается завершённым.

На практике при использовании СПС возникает необходимость достижения минимальной зависимости одних характеристик от других. Например, регулирование задержки не должно сопровождаться существенным изменением формы амплитудно-частотной характеристики (АЧХ) в полосе частот, а регулирование АЧХ не должно вызывать изменение фазового сдвига. Учёт требования неизменности фазового сдвига при регулировании необходим при проектировании передатчиков с суммированием мощности, модулей активных фазированных решеток, прецизионных широкополосных усилителей, аттенюаторов и других устройств. Изменение фазового сдвига обусловлено влиянием паразитных реактивностей управляемых элементов. Их технологическое уменьшение связано со значительными трудностями. Поэтому на практике активно используется компенсация паразитных реактивностей управляемых элементов схемотехническим путем.

Аттенюаторы, выполненные на основе Г-, Т- и П-образного соединения последовательно и параллельно включённых диодов получили наибольшее распространение. Сопротивление диодов под воздействием управляющего тока может меняться в широких пределах, что позволяет изменять АЧХ и затухание в тракте. Независимость фазового сдвига при регулировании затухания в таких аттенюаторах достигается с помощью реактивных цепей, включенных в базовую структуру. Очевидно, что при разном соотношении сопротивлений параллельных и последовательных диодов может быть получен один и тот же уровень вносимого ослабления. Но изменение фазового сдвига будет различным.

Исследуем возможность упрощения автоматизированного проектирования аттенюаторов, исключающего двойную оптимизацию корректирующих цепей и параметров управляемых элементов. В качестве исследуемой СПС будем использовать электрически управляемый аттенюатор, схема замещения которого приведена на рис. 8.8. Минимальный уровень затухания обеспечивается в случае малого сопротивления элемента Rs и большого сопротивления элемента Rp. По мере увеличения сопротивления элемента Rs и уменьшения сопротивления элемента Rp вносимое ослабление увеличивается.

Линии передачи l1, l2, l3 обеспечивают фазовую инвариантность отклика относительно входного воздействия. Распределенные индуктивность и ёмкость линий комбинируются с паразитными параметрами L, C управляемых элементов, например, диодов, и компенсируют изменение фазового сдвига при регулировке ослабления.

Для компьютерного моделирования была использована схема замещения диода со следующими параметрами: ёмкость перехода C=0,02 пФ, индуктивность выводов L=0,16 нГн, сопротивление растекания не учитывалось ввиду его малости. Заметим, что паразитные реактивные параметры управляемых элементов являются основной причиной, ограничивающей полосу рабочих частот. Объёмные сопротивления Rs и Rp изменялись от 3 до 200 Ом. Сопротивления генератора и нагрузки, а также резистора R равны 50 Ом. В результате оптимизации по критерию минимума фазового сдвига были найдены параметры коррекции – длины линий передачи l и их волновые сопротивления: l1=3 мм, l2=1,1 см, l3=2 мм, p1=70 Ом, p2=75 Ом, p3=40 Ом. Рассчитывались вносимое затухание A(w) в зависимости от круговой частоты (величина, обратная АЧХ) и изменение фазового сдвига f(w), то есть разность фаз при начальном (A0) и выбранном уровне ослабления (Ai).

Зависимости изменения фазового сдвига от частоты и затухания для схемы без коррекции и с коррекцией приведены на рис. 8.9 и 8.10 соответственно. В корректированном аттенюаторе в диапазоне ослаблений 1,3-7,7 дБ и полосе частот 0,01?4,0 ГГц достигнуто изменение фазового сдвига не более 0,2°. В аттенюаторе без коррекции изменение фазового сдвига в той же полосе частот и диапазоне ослаблений достигает 3°. Таким образом, фазовый сдвиг уменьшен за счет коррекции почти в 15 раз.

Будем считать параметры коррекции и управления независимыми переменными или факторами, влияющими на затухание и изменение фазового сдвига. Это даёт возможность с помощью системы Statistica провести факторный и регрессионный анализ СПС с целью установления физических закономерностей между параметрами цепи и отдельными характеристиками, а также упрощения поиска оптимальных параметров схемы.

Исходные данные формировались следующим образом. Для параметров коррекции и сопротивлений управления, отличающихся от оптимальных в большую и меньшую стороны на сетке частот 0,01?4 ГГц, были вычислены вносимое ослабление и изменение фазового сдвига.

График факторных нагрузок, построенный для двух факторов, показывает, что параметры коррекции и параметры управления чётко разделены в своем влиянии на характеристики аттенюатора.

Факторные модели для изменения фазового сдвига и вносимого затухания были построены с помощью модуля "общие регрессионные модели – факторная регрессия". В результате моделирования найдены коэффициенты факторной регрессии, которые представлены в виде столбчатых диаграмм на рис. По величине коэффициентов факторной регрессии можно судить о влиянии того или иного параметра на соответствующую характеристику устройства.

Построенные факторные модели не учитывают влияния паразитных параметров управляемых элементов и их линейных комбинаций с остальными элементами и частотой. Тем не менее, усложнять модель нецелесообразно, так как целью моделирования не являлся поиск параметров, для которых изменение фазового сдвига минимально, а требовалось только оценить влияние каждого элемента на характеристики устройства. По результатам анализа можно сделать выводы о влиянии параметров коррекции и управления на изменение фазового сдвига и затухания, а также подтвердить физические предположения о работе схемы.

1. На изменение фазового сдвига в первую очередь влияют параметры управления (см. рис. 8.12, наибольшие коэффициенты для Rp и Rs). Этот вывод не очевиден, так как, например, ранее считалось, что основной вклад в изменение фазового сдвига вносят паразитные параметры управляемых элементов.
2. Стабилизацию фазы обеспечивают корректирующие линии l3 и l1. Влияние линии l2 статистически незначимо, и её можно исключить из схемы без существенного ухудшения характеристик.
3. Параллельно включенный управляемый элемент сильнее всего влияет как на изменение фазы, так и на рабочее затухание (см. рис. 8.12 и 8.13, наибольшие коэффициенты для Rp равны 31,849 и 47,200 соответственно).
4. Оба управляемых элемента в равной степени оказывают влияние на вносимое ослабление. Следовательно, формирование закона управления для Rp и Rs принципиально необходимо для повышения точностных характеристик устройства. Влияние остальных параметров, в том числе линии l2 на ослабление незначимо по уровню 0,05.

Методы статистического моделирования, в частности, факторный и регрессионный анализ, которые раньше не использовались для проектирования дискретных устройств с переменными состояниями, позволяют выявить физические закономерности работы элементов системы. Это способствует созданию структуры устройства исходя из заданного критерия оптимальности. В частности, в данном разделе рассматривался фазоинвариантный аттенюатор как типичный пример системы с переменными состояниями. Выявление и интерпретация факторных нагрузок, влияющих на различные исследуемые характеристики, позволяет изменить традиционную методологию и существенно упростить поиск параметров коррекции и параметров регулирования.

Установлено, что использование статистического подхода к проектированию подобных устройств оправдано как для оценки физики их работы, так и для обоснования принципиальных схем. Статистическое моделирование позволяет существенно сократить объём экспериментальных исследований.


Результаты

• Наблюдение за общими факторами и соответствующими факторными нагрузками – это необходимое выявление внутренних закономерностей процессов.
• С целью определения критических значений контролируемых расстояний между факторными нагрузками следует накапливать и обобщать результаты факторного анализа для однотипных процессов.
• Применение факторного анализа не ограничено физическими особенностями процессов. Факторный анализ является как мощным методом мониторинга процессов, так и применим к проектированию систем самого различного назначения.