ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Основные понятия

Во многих случаях требуется решить, справедливо ли некоторое суждение. Например, верно ли, что два набора данных исходят из одного и того же источника? Что А – лучший работник, чем В? Что от дома до работы быстрее дойти пешком, а не доехать на автобусе и т. д. Если мы считаем, что исходные данные для таких суждений в той или иной мере носят случайный характер, то и ответы можно дать лишь с определенной степенью уверенности, и имеется некоторая вероятность ошибиться. Поэтому при ответе на подобные вопросы хотелось бы не только уметь принимать наиболее обоснованные решения, но и оценивать вероятность ошибочности принятого решения.

Рассмотрение таких задач в строгой математической постановке приводит к понятию статистической гипотезы. В этой главе рассматриваются вопросы о том, что такое статистические гипотезы и какие существуют способы их проверки.

Статистические модели

Весь статистический анализ основан на идее случайного выбора. Мы понимаем, что имеющиеся данные появились как результат случайного выбора из некоторой генеральной совокупности, нередко – воображаемой. Обычно мы полагаем, что этот случайный выбор произведен природой. Впрочем, во многих задачах эта генеральная совокупность вполне реальна, и выбор из нее произведен исследователем.

Поскольку мы приняли вероятностную точку зрения на происхождение наших данных (т. е. считаем, что они получены путем случайного выбора), то все дальнейшие суждения, основанные на этих данных, будут иметь вероятностный характер. Всякое утверждение будет верным лишь с некоторой вероятностью. И с некоторой вероятностью оно может оказаться неверным.
Какую вероятность следует считать малой? На этот вопрос нельзя дать количественного ответа, пригодного во всех случаях. Ответ зависит от того, какой опасностью грозит нам ошибка. При проверке статистических гипотез, например, полагают малыми вероятности, начиная с 0,05–0,01.

Статистические гипотезы

Термин "гипотеза" означает предположение, которое не только вызывает сомнения, но и которое мы собираемся в данный момент проверить.

Нулевая гипотеза H0 – это гипотеза об отсутствии различий. Это то, что мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий

Она содержит число 0: x1-x2=0, где x1 и x2 – сопоставляемые значения признаков.

Альтернативная гипотеза H1– это гипотеза о значимости различий. Это то, что мы хотим доказать, поэтому иногда её называют экспериментальной гипотезой

Бывают задачи, когда мы хотим доказать незначимость различий, т. е. подтвердить нулевую гипотезу. Однако чаще требуется доказать значимость различий, ибо они более информативны в поиске нового.
Проверка гипотез осуществляется с помощью критериев статистической оценки различий.

Статистические критерии

Если гипотезу можно проверить непосредственно, не возникает никаких проблем. Но если прямого способа проверки нет, приходится прибегать к проверкам косвенным. Это значит, что приходится довольствоваться проверкой некоторых следствий, которые логически вытекают из гипотезы. Если некоторое явление логически неизбежно следует гипотезы, но в природе не наблюдается, то это значит, что гипотеза неверна. С другой стороны, если происходит то, что при гипотезе происходить не должно, это тоже означает ложность гипотезы. Заметим, что подтверждение следствия ещё не означает справедливости гипотезы, поскольку правильное заключение может вытекать и из неверной предпосылки.

Статистический критерий – это правило, по которому принимается решение о приня-тии истинной и отклонении ложной гипотезы с высокой вероятностью. Критерии делятся на параметрические и непараметрические.

Параметрические критерии – это критерии, включающие в формулу расчёта параметры распределения, т. е. средние и дисперсии (t-критерий Стьюдента, критерий F и др.).

Непараметрические критерии – это критерии, не включающие в формулу расчёта параметров распределения и основанные на оперировании частотами или рангами (Q-критерий Розенбаума, критерий Уилкоксона и др.).

При нормальном распределении признака параметрические критерии обладают большей мощностью, чем непараметрические критерии. Они способны отвергать нулевую гипотезу, если она неверна. Поэтому во всех случаях, когда сравниваемые выборки взяты из нормально распределяющихся совокупностей, следует отдавать предпочтение параметрическим критериям.

В случае очень больших отличий распределений признака от нормального вида следует применять непараметрические критерии, которые в этой ситуации оказываются часто более мощными. В ситуациях, когда варьирующие признаки выражаются не в численной форме, применение непараметрических критериев оказывается единственно возможным.

Проверка гипотез с помощью критериев

Схема проверки гипотез с помощью статистических критериев состоит из следующих трёх шагов.
1. Вычисляется эмпирическое (или фактическое, реальное) значение критерия Fэмп. Вычисляется число степеней свободы и уровень значимости.
2. По таблицам критических значений для выбранного критерия находится так называемая критическая точка (или критическое значение) Fкр.
3. По соотношению эмпирического и критического значений критерия судят о том, подтверждается или опровергается нулевая гипотеза. Например, если Fэмп > Fкр, гипотеза H0 отвергается.

Критические значения критерия берутся из статистических таблиц

В большинстве случаев для того, чтобы различия признавались значимыми, необходимо, чтобы эмпирическое значение критерия превышало критическое, хотя есть критерии (например, Манна-Уитни или критерий знаков), а которых нужно придерживаться противоположного правила.
Число степеней свободы равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий относятся объём выборки, средние и дисперсии.

Уровень значимости – это вероятность отклонения нулевой гипотезы, в то время как она верна

Обычно при проверке статистических гипотез принимают три уровня значимости: 5 %-й (вероятность ошибочной оценки р=0,05), 1 %-й (р=0,01) и 0,1 %-й (р=0,001). В промышленной статистике часто считают достаточным 5 %-й уровень значимости. При этом нулевую гипотезу не отвергают, если в результате исследования окажется, что вероятность ошибочности оценки относительно правильности принятой гипотезы превышает 5 %, т.е. р>0,05. Если же р<0,05, то принятую гипотезу следует отвергнуть на взятом уровне значимости, Ошибка при этом возможна не более чем в 5 % случаев, т. е. она маловероятна. При более ответственных исследованиях уровень значимости может быть уменьшен до 1 % или даже до 0,1 %.

В пакете Statistica значение задаваемого уровня значимости не используется. Как правило, в выходных данных содержатся выборочные значения статистики критерия и вероятность того, что случайная величина превышает это выборочное значение при условии, что верна гипотеза H0. Эта вероятность называется р-значением (p-level).

Ошибки при принятии гипотез

Ошибка, состоящая в том, что правильная гипотеза отклонена, в то время как она верна, называется ошибкой I рода Ошибка, состоящая в том, что правильная гипотеза принята, в то время как она неверна, называется ошибкой II рода

Последствия этих ошибок могут сильно различаться по их значимости. Рассмотрим это на следующем простом примере. Пусть, например, проверяется партия медикаментов сильного действия на соответствие требованиям и действительно правильное решение о том, что партия требованиям соответствует, ошибочно отвергается (ошибка первого рода). В этом случае последствием будет только материальный ущерб предприятию, так как партия бракуется. Если же на самом деле партия требованиям не удовлетворяет, но ошибочно принята (ошибка второго рода), то это повлечет нанесение ущерба здоровью людей и даже возможную их гибель из-за передозировки, поскольку речь идет о сильнодействующем лекарстве.

При приёмочном контроле ошибка первого рода приводит к браковке партии с допустимой долей брака (риск производителя). При контроле производства – к вмешательству в налаженный процесс производства (ложная тревога). Ошибка второго рода приводит к принятию партии с недопустимой долей брака (риск потребителя). При контроле производства – приводит к вмешательству в процесс производства, вышедший за допустимые границы (пропуск перехода).
Вероятность появления ошибки первого рода обозначается буквой ?, второго рода ? ?. Следовательно, вероятность правильного решения равна 1-?.Вероятность ? является уровнем значимости критерия. Классификация результатов при проверке статистических гипотез приведена в табл.

Таблица
Виды ошибок при проверке статистических гипотез

При заданной вероятности ошибки первого рода α вероятность ошибки второго рода может быть уменьшена за счёт увеличения объёма выборки.

Двусторонний критерий для среднего значения с нормальным распределением и известной дисперсией

Для проверки гипотез о средних рекомендуется использовать таблицу.

Таблица
Проверка гипотез о средних

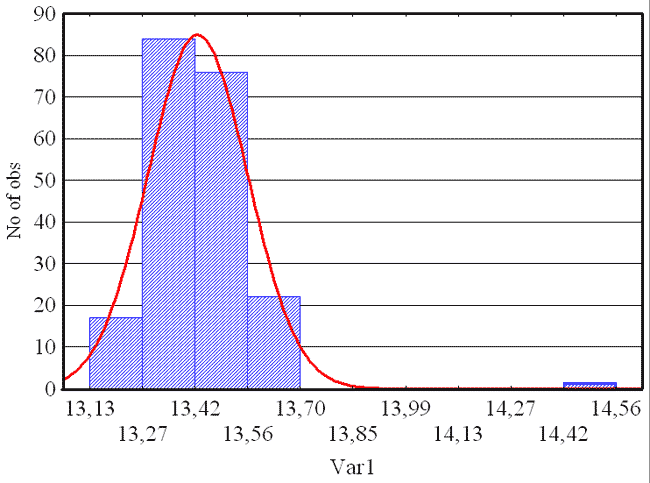
Рассмотрим следующий пример. Пусть значения диаметров стальных стержней, используемых для изготовления колец подшипников, распределяются по нормальному закону при =0,12 мм. Желательно, чтобы стержни имели диаметр 1,50 мм, причём отклонение от этой величины как в одну, так и в другую сторону нежелательны. Желательно, чтобы отбраковывалось не более 10 % всех партий, для которых среднее значение диаметров стержней равно 1,50 мм. Из очень большой партии делается выборка из 75 стержней. Выборочное среднее равно =1,54 мм. Должна ли партия быть принята?

Для решения формулируем гипотезы:
Но: μ=μо, где о=1,50 мм
Н1: μо
Устанавливаем уровень значимости: μо=0,10.
Определяем область отклонения (браковки):
стандартная ошибка среднего: , т.к. нормированному отклонению нормальной случайной величины, ограниченному таким образом, что с каждого края кривой распределения исключается 5 % площади, соответствует величина 1,645, то находим: . То есть область принятия задаётся как . Такая проверка называется двусторонней, т.к. область отклонений лежит по обеим сторонам от μо.
Принимаем решение: т.к. среднее выборки лежит в области отклонения, то гипотеза μо=1,50 мм отклоняется, т.е. партию необходимо забраковать.

Односторонний критерий для биномиального распределения доли дефектных изделий

Пусть была сделана случайная выборка объёмом 20 изделий, одно из которых оказалось дефектным. Следует ли считать процесс правильным или ход процесса отклонился от нормы и должен быть остановлен? Желательно, чтобы в ходе процесса браковалось не более 4 % изделий. Согласимся пойти на 5 % риск необоснованной браковки такого процесса.
Формулируем гипотезы:
Но: Р=Р1, где Р1=0,04
Н1: Р>P1
Устанавливаем уровень значимости: 1 0,05.
Определяем область отклонения (браковки). Эта область определяется числом членов разложения бинома (P1+Q1)n=(0,04+0,96)20, соответствующих значению интегральной вероятности 1=1-1=0,95, т.е. определяется из равенства: . Воспользовавшись таблицами интегрального биномиального распределения вероятностей для n=20, P=0,04, определяем для вероятности 0,95, что приёмочное число А=2, браковочное число R=3, а область отклонения определяется соотношением d3. Такая проверка называется односторонней, т.к. область отклонений лежит в одну сторону от Р1.

Это значение можно вычислить с помощью вероятностного калькулятора Statistics/ Probability calculator/ Distributions

Принимаем решение: т.к. приёмочное число равно 2, а в выборке имеется только одно бракованное изделие, то принимается гипотеза Н1 ? процесс идёт правильно.

Проверка гипотез о виде распределения

При проверке гипотез о параметрах генеральной совокупности контролируемого показателя предполагается, что закон распределения известен. Однако на практике это не всегда имеет место. И тогда необходимо определить, какому закону распределения подчиняется исследуемая случайная величина.

В конкретных задачах, как правило, всегда имеется некоторое основание предполагать, что закон распределения имеет определенный вид F (например, нормальный, Рэлея, Пуассона и т.д.). Это предположение может быть сделано, например, на основе построения гистограммы или на основе физического смысла исследуемого показателя.

В этом случае необходимо проверить гипотезу Н0: генеральная совокупность распределена по закону F. Конкурирующей гипотезой будет гипотеза Н1: генеральная совокупность не распределена по закону F.
Для решения этой задачи используют статистические критерии, называемые критериями согласия.
Теория вероятностей позволяет пользоваться несколькими критериями согласия: критерий Пирсона (критерий x2), критерий Колмогорова, Смирнова и др.
Здесь ограничимся только проверкой гипотез с помощью критерия Пирсона. Его достоинство по сравнению с другими критериями состоит в том, что он может быть применен к самым различным законам распределения, тогда как другие критерии применимы только к вполне определенным законам.

Критерий Пирсона выгодно отличается от остальных инвариантностью к закону распределения

Пусть имеется выборка наблюдений случайной величины. Проверяется гипотеза H0, утверждающая, что случайная величина имеет функцию распределения F(x). Проверка гипотезы H0 при помощи критерия ?2 в системе Statistica осуществляется по следующей схеме.
1. Формируются исходные данные, состоящие из n наблюдений одной переменной Var 1. В качестве примера возьмём результаты измерения диаметров заклёпок – 200 наблюдений:

13,39 13,33 13,56 13,38 13,43 13,37 13,53 13,40 13,25 13,37
13,28 13,34 13,50 13,38 13,38 13,45 13,47 13,62 13,45 13,39
13,53 13,58 13,32 13,27 13,42 13,40 13,57 13,46 13,33 13,40
13,57 13,36 13,43 13,38 13,26 13,52 13,35 13,29 13,48 13,43
13,40 13,39 13,50 13,52 13,39 13,39 13,46 13,29 13,55 13,31
13,29 13,33 13,38 13,61 13,55 13,40 13,20 13,31 13,46 13,13
13,43 13,51 13,50 13,38 13,44 13,62 13,42 13,54 13,31 13,58
13,41 13,49 13,42 13,45 13,34 13,47 13,48 13,59 13,20 14,56
13,55 13,44 13,50 13,40 13,48 13,29 13,31 13,42 13,32 13,48
13,43 13,26 13,58 13,38 13,48 13,45 13,29 13,32 13,24 13,38
13,34 13,14 13,31 13,51 13,59 13,32 13,52 13,57 13,62 13,29
13,23 13,37 13,64 13,30 13,40 13,58 13,24 13,32 13,52 13,50
13,43 13,58 13,63 13,48 13,34 13,37 13,18 13,50 13,45 13,60
13,38 13,33 13,57 13,28 13,32 13,40 13,40 13,33 13,20 13,44
13,34 13,54 13,40 13,47 13,28 13,41 13,39 13,48 13,42 13,46
13,28 13,46 13,37 13,53 13,43 13,30 13,45 13,40 13,45 13,40
13,33 13,39 13,56 13,46 13,26 13,35 13,42 13,36 13,44 13,41
13,43 13,51 13,51 13,24 13,34 13,28 13,37 13,54 13,43 13,35
13,52 13,23 13,48 13,48 13,54 13,41 13,51 13,44 13,36 13,36
13,53 13,44 13,69 13,66 13,32 13,26 13,51 13,38 13,46 13,34

2. По команде Statistics/ Distribution Fitting в стартовом окне выбираем вид случайной величины – непрерывная (Continuous Distributions, установлена по умолчанию) или дискретная (Discrete Distributions), вид распределения (по умолчанию предлагается нормальное), OK. Кнопкой Variables выбираем переменную.

Понятно, что если требуется проверить соответствие другому закону распределения, надо выбрать его из предложенного списка

3. Во вкладке Parameters того же окна (рис. 10.1) появятся оценки параметров. Число интервалов группировки (Number of categories) можно при необходимости изменить. Нажмите кнопку Summary.

4. На экран выводится таблица для расчёта статистики критерия – распределение случайной величины по интервалам. В таблице частот нужны столбцы Observed Frequency (наблюдаемые частоты) и Expected Frequency (ожидаемые частоты). Сравним графически наблюдаемые и ожидаемые частоты: запишем соответствующие столбцы в таблицу данных и построим график рассеяния (команды Graphs/ Scatterplots/ Variables/ OK). Наблюдаем существенное различие между переменными, так как точки плохо укладываются на прямую линию.

Вверху таблицы выводится значение статистики критерия x2 (Chi-Square), число степеней свободы (df) и вычисленный уровень значимости p-level. Для нашего примера получено:

Variable: Var1, Distribution: Normal
Chi-Square = 11,99951, df = 3 (adjusted), p = 0,0073.

Значение вероятности p=P(?23> 11,999)=0,007 означает, что если гипотеза верна, вероятность получить 12 или больше равна 0,007. Это слишком мало, чтобы поверить в нормальность распределения. Гипотезу о нормальности отклоняем.
Если посмотреть гистограмму наблюдений (рис 10.3), видно, что в выборке имеется одно аномальное значение 14,56 (188-е по счёту), которое могло появиться в результате какой-либо ошибки (при записи наблюдений, при перепечатке или попалась деталь с другого станка и т.д.). Удалим его и снова проверим гипотезу.

Удаление одного наблюдения, если оно типично, не может изменить характеристики совокупности из 200 элементов. Если же изменение происходит, это наблюдение типичным не является и должно быть удалено. Если повторить проверку гипотезы для ?цензурированной? выборки, можно убедиться в том, что наблюдения не противоречат гипотезе о нормальности.

Проверка гипотез об однородности выборок

Пусть имеются выборки, извлечённые из различных совокупностей. Требуется проверить гипотезу о том, что исходные совокупности распределены одинаково. В системе Statistica эта гипотеза проверяется в модуле Statistics/ Advanced Linear/Nonlinear models/ Log-Linear Analysis of Frequency Tables.
Пусть, к примеру, имеются данные о наличии примесей (P1–P4) в углеродистой стали, выплавляемой двумя заводами Z1, Z2.

Проверим гипотезу о том, что распределения содержания нежелательной примеси одинаковы на этих заводах.
1. В строке Input file: выбираем Frequencies w/out coding variables (частоты без кодирующих переменных). Кнопкой Variables вводим все переменные (Select all). Кнопкой Specify Table (спецификация таблицы) в ячейках No. of levels: вводим 4 и 2 (рис. 10.5).

2. Дважды нажимаем OK и во вкладке Advanced получившегося окна выполним Test all marginal & partial association models.
3. В таблице Results of Fitting all K-Factor Interactions в последней строке получаем столбца значение статистики критерия x2 (Chi-Square), равное 3,59, число степеней свободы (Degrs. of Freedom) df=3 и уровень значимости 0,30887. Эта величина не больше критической (см. Приложение 2). Следовательно, гипотезу об одинаковом распределении содержания примеси в металле на двух заводах можно принять.

Результаты

• Из вероятностного характера данных следует вероятностная природа принимаемых решений.
• Методы проверки статистических гипотез позволяют не только принимать научно обоснованные решения, но и оценивать вероятность ошибки.
• Статистический критерий ? это правило, по которому принимается решение о принятии истинной и отклонении ложной гипотезы с высокой вероятностью.
• Проверка гипотез требует от исследователя знания теории вероятностей и умения пользоваться статистическими таблицами.
• Проверка данных на соответствие нормальному закону распределения очень важна для данных промышленной статистики, так как большинство статистических методов, используемые в промышленных приложениях, в частности, "семь простых инструментов", основаны на принадлежности данных нормальному закону распределения.