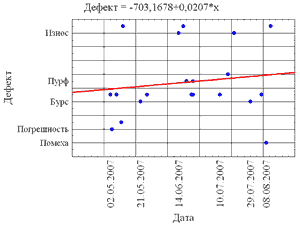
Разведочный визуальный анализ данных

Начало

Графический анализ данных

Визуальные методы анализа данных чрезвычайно важны для предварительного исследования. Многие скрытые явления становятся отчётливыми, если для них найти подходящее графическое представление. Кроме того, многие сложные задачи решаются чрезвычайно простыми методами описательной статистики.

Лучшим способом наглядного представления данных является графический анализ. Данный метод является важным орудием науки, особенно в статистических и экономических исследованиях.

График – это чертёж, показывающий соотношение статистических величин при помощи разнообразных геометрических и изобразительных средств. Опция Graphs позволяет построить различные виды графиков. Рассмотрим наиболее распространённые из них.

Диаграмма рассеяния

Диаграммой рассеяния называется представление элементов выборки как точек на плоскости. Диаграмма строится по команде Graphs/ Scatterplots. В появившемся окне необходимо нажать кнопку Variables: и указать переменные – аргумент и функцию. Во вкладке Advanced можно указать тип подгоночной функции (Fit) или отключить её (Off). Опция Graphtype: позволяет построить множество графиков на разных (Regular) или одной (Multiple) сетке.

Построим диаграмму рассеяния для данных из таблицы. Прямая на диаграмме рассеяния – это график простой линейной регрессии у=–703,1678+0,0207х.

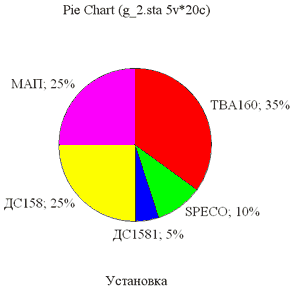
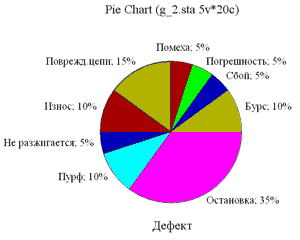
Трёхмерный визуальный анализ данных

Трёхмерный визуальный анализ позволяет наглядно анализировать данные в трёхмерном пространстве, например, строить трёхмерное изображение последовательностей исходных данных (наблюдений) для одной или нескольких выбранных переменных (рис. 2.10). Трёхмерные представления значений каждой переменной не перекрываются, как на двухмерном графике, а строятся как значения какой-то поверхности в пространстве. С помощью трёхмерного визуального анализа можно обнаружить сложные нелинейные взаимосвязи между переменными.

Здесь рассмотрено практическое применение трёхмерного визуального анализа на примере моделирования процесса микроплазменного электрохимического нанесения покрытий на алюминиевых сплавах путём обработки экспериментальных результатов в программе Statistica.

Зная исходную функцию, можно построить любой график, как двумерный, так и трёхмерный. В отличие от большинства других типов графиков, для пользовательского графика не требуется выбирать переменные. Вместо этого для построения графика программа запросит ввод формулы.

Круговые диаграммы

Круговые диаграммы (Pie Charts) весьма показательны, когда количество данных невелико. На круговой диаграмме данные представлены в процентах. Построим круговые диаграммы для примера (табл.), указав в окне выбора переменных сразу две переменные: «Установка» и «Дефект».

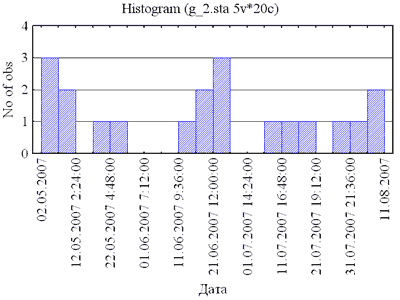
По построенным круговым диаграммам легко определить установку, вызвавшую большинство ремонтных остановок за эксплуатационный период май–август 2007 года. Это ТВА160 – 35% от всех остановок заводов.

Построение гистограмм

Любой производственный процесс характеризуется определённым распределением заданного показателя качества продукции. Это распределение обусловлено его физической природой, условиями реализации и множеством случайных и неслучайных факторов, действующих на процесс. Знание того, каким является реальный процесс, позволяет принимать необходимое управленческое решение с целью выявления и последующего устранения причин, ухудшающих характеристики процесса, и с целью его дальнейшего совершенствования.

Представление о реальном процессе можно получить путём построения гистограмм. Часто первый шаг визуального анализа данных состоит в построении гистограмм для всех переменных.

Гистограммой называется ступенчатая диаграмма, которая строится для исследуемого показателя на основе выборки. Она состоит из прямоугольников, горизонтальные стороны которых равны частичным интервалам, а вертикальные – числу измеренных объектов, показатель которых  попал в тот или иной интервал. Частичные интервалы – это малые отрезки, на которые разбивается область возможных значений показателя.

Гистограммы позволяют увидеть, как распределены значения переменных по интервалам группировки, то есть как часто переменные принимают значения из различных интервалов. Гистограмма наглядно показывает, какие диапазоны значений исследуемой переменной являются наиболее частыми, насколько сильно они различаются между собой, как сконцентрировано большинство наблюдений вокруг среднего, является распределение симметричным или нет, имеет ли оно одну моду или несколько мод, то есть является мультимодальным.

Для построения гистограммы в программе Statistica можно воспользоваться командой Graphs / 2D Graphs / Histograms. Раскроется диалоговое окно. Прежде всего, в этом окне следует определиться с именем переменной, для которой будет строиться гистограмма. Для этого нужно кликнуть слева вверху окна по клавише Variables: и среди появившегося списка выбрать требуемую переменную. Результат выбора можно отследить в поле Vars:. Затем в поле Graph Type: следует выбрать графический тип гистограммы. По умолчанию установлен обычный (Regular).

Далее в поле Categories (классы) нужно определиться с типом классов группировки. Если данные дискретны (прерывисты, например, как у пуассоновской выборки), то кнопкой лучше задать режим IntegerMode. При этом гистограмма будет представлять собой оценку, где классами будут служить встретившиеся в выборке номиналы. Если данные непрерывны (например, как у нормальной или равномерной выборки), то кнопкой следует выбрать режим Categories:. При отмеченном чекбоксе у статуса Auto это означает, что данные будут сгруппированы по классам одинаковой длины в пределах выборочного размаха. Причём число классов здесь нужно указать в соответствующем окне с цифрами. Как число, так и границы классов у гистограммы можно задать произвольными. Для этого следует использовать опцию Boundaries:.

Наконец в поле Fit Type: по линейке прокрутки можно выбрать вид ожидаемой подгоночной кривой к графику гистограммы. К примеру, для нормальной выборки логично выбрать гауссоиду Normal; а для пуассоновской выборки логично указатьPoisson; но для равномерной выборки следует задать Off, поскольку форма плотности распределения здесь очевидна и отображать её не следует.

Гистограмма строится по клавише OK в правом верхнем углу окна. Построим гистограмму для переменной «Дата» из табл.

Наконец в поле Fit Type: по линейке прокрутки можно выбрать вид ожидаемой подгоночной кривой к графику гистограммы. К примеру, для нормальной выборки логично выбрать гауссоиду Normal; а для пуассоновской выборки логично указать Poisson; но для равномерной выборки следует задать Off, поскольку форма плотности распределения здесь очевидна и отображать её не следует. Гистограмма строится по клавише OK в правом верхнем углу окна. Построим гистограмму для переменной «Дата» из табл.

Видим, что наибольшее число поломок оборудования было в первой декаде мая и в последнюю неделю июня. Хорошо погуляли! Как отдыхаем, так и живём.

С помощью специальных статистических критериев, например, с помощью критерия хи-квадрат, можно удостовериться, насколько правилен этот вывод. В данном примере различие между случаями отказов оборудования небольшое, но и число наблюдений мало. Если бы подобное различие имело место для 100 дней, то, очевидно, мы отнесли бы его на счёт случайной ошибки и не приняли бы во внимание.

В разведочном анализе данных гистограмма – обязательный шаг. Гистограмма представляет интерес по следующим причинам:

• по форме распределения можно охарактеризовать природу исследуемой переменной (например, бимодальность распределения может означать, что выборка неоднородна и состоит из наблюдений, принадлежащих двум различным множествам;
• многие статистики критериев основаны на определенных предположениях о виде распределения. Гистограммы помогают визуально проверить выполнение этих предположений. 

Построение гистограммы является быстрым и наглядным методом получения информации о виде и характере процесса на основе относительно небольшого объёма выборки. Это обусловливает его широкое применение при анализе, настройке и наладке процесса и позволяет в дальнейшем в случае необходимости применять по отношению к процессу целенаправленные предупреждающие или корректирующие управляющие воздействия.