| Тренинги и семинары | Проекты | Статьи | Фотографии | Услуги | Контакты | IEEE | О центре |
ДИСКРИМИНАНТНЫЙ АНАЛИЗОбщие сведения Дискриминантный анализ используется для принятия решения о том, какие переменные различают (дискриминируют) две или более возникающие совокупности (группы). В дискриминантном анализе рассматривается некоторая «зависимая» переменная, определяющая наше мнение относительно предстоящей группировки. Далее определяются линейные классификационные модели, которые позволяет «предсказать» поведение новых элементов в терминах зависимой переменной на основании измерения ряда независимых переменных (факторов, показателей), которыми они характеризуются. Отличие дискриминантногоанализа от кластерного Например, предположим, что проводится маркетинговое исследование. Выявлено три уровня предпочтений потребителя к определенной марке товара и есть измерения ряда показателей его стиля жизни. Строятся линейные модели, в которых подстановка значений из стилевых переменных сможет дать ответ на вопрос о предпочтении потребителя данного вида товара. Эта модель более информативна, чем, например, модель в кластерном анализе, так как дает ?силу влияния?. Поэтому в маркетинге дискриминантный анализ часто используется в априорной сегментации рынка, в отличие от кластерного анализа, который используется для апостериорной сегментации. Психиатр может регистрировать различные переменные, относящиеся к состоянию больного шизофренией, чтобы выяснить, какие переменные лучше предсказывают, что пациент, вероятно, выздоровел полностью (группа 1), частично (группа 2) или совсем не выздоровел (группа 3). Биолог может записать различные характеристики сходных типов (групп) цветов, чтобы затем провести анализ дискриминантной функции, наилучшим образом разделяющей типы или группы. Общая модель дискриминантного анализа Вероятно, наиболее общим применением дискриминантного анализа является включение в исследование многих переменных с целью определения тех из них, которые наилучшим образом разделяют совокупности между собой. Например, исследователь в области образования, интересующийся предсказанием выбора, который сделают выпускники средней школы относительно своего дальнейшего образования, произведёт с целью получения наиболее точных прогнозов регистрацию возможно большего количества параметров обучающихся, например, мотивацию, академическую успеваемость и т.д. Другими словами, нужно построить модель, позволяющую лучше всего предсказать, к какой совокупности будет принадлежать тот или иной образец. Виды дискриминантного анализа Пошаговый анализ с включением. В пошаговом анализе дискриминантных функций модель дискриминации строится по шагам. Точнее, на каждом шаге просматриваются все переменные и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная должна быть включена в модель на данном шаге, и происходит переход к следующему шагу. Пошаговый анализ с исключением. Можно также двигаться в обратном направлении. В этом случае все переменные будут сначала включены в модель, а затем на каждом шаге будут устраняться переменные, вносящие малый вклад в предсказания. Тогда в качестве результата успешного анализа можно сохранить только ?важные? переменные в модели, то есть те переменные, чей вклад в дискриминацию больше остальных. F для включения, F для исключения. Эта пошаговая процедура руководствуется соответствующим значением F для включения и соответствующим значением F для исключения. Значение F-статистики для переменной указывает на её статистическую значимость при дискриминации между совокупностями, то есть она является мерой вклада переменной в предсказание членства в совокупности. Дискриминантный анализ в системе Statistica Рассмотрим решение практической задачи сегментации товаров по группам методом дискриминантного анализа в системе Statistica. Исходные данные представлены в табл. В этой таблице Var 1–Var 5 – это различные показатели качества и стоимости, а Class – к какому классу был отнесён товар экспертным способом. Таблица 11.1
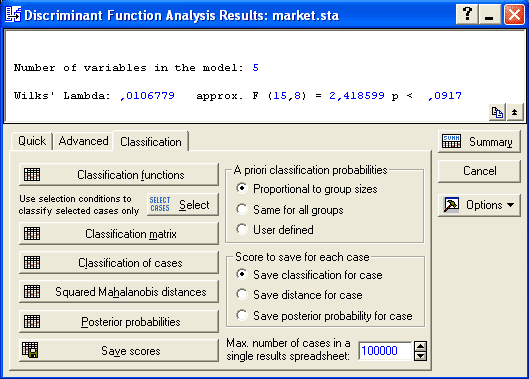
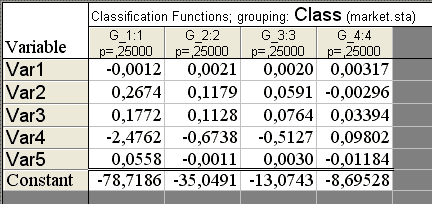
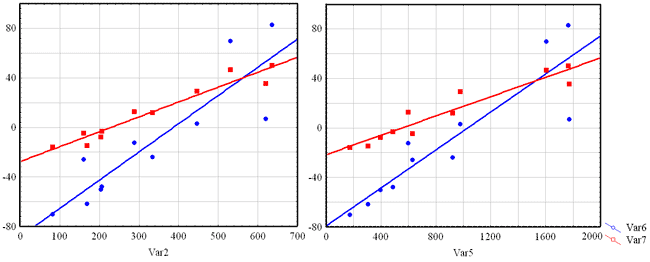
1. Открыть модуль Statistics/ Multivariable Exploratory Techniques/ Discriminant Analysis. Нажать ОК, в результате чего появится стартовая панель модуля Discriminant Function Analysis. 2. Кнопка Variables позволяет выбрать Grouping variable (группируемую переменную) и Independent variable list (независимые переменные). Имена переменных в левой и правой части не должны пересекаться. Codes for grouping variable (Коды для групп переменной) указывают количество анализируемых групп объектов. Missing data (пропущенные переменные) позволяет выбрать построчное удаление переменных из списка, либо заменить их на средние значения. 3. После нажатия кнопки ОК откроется диалоговое окно с результатами, которые представлены в окне Discriminant Function Analisis Results (результаты анализа дискриминантных функций) (рис. 2). Верхняя информационная часть диалогового окна сообщает, что: Из классификационной матрицы можно сделать вывод, что объекты в классах 1, 2, 4 были правильно отнесены экспертным способом к выделенным группам. В классе 3 есть объекты, неправильно отнесённые к соответствующим группам. Их можно посмотреть, нажав в окне на рис. 2 кнопку Classification of cases (классификация наблюдений). В таблице классификации наблюдений некорректно отнесенные предприятия помечаются звёздочкой (*). Таким образом, задача получения корректных выборок состоит в том, чтобы исключить из выборок те объекты, которые по своим показателям не соответствуют большинству предприятий, образующих однородную группу. Для этого с помощью метрики Махаланобиса определятся расстояние от всех объектов до центра тяжести каждой группы. Отнесение экспертом объекта в группу считается ошибочным, если расстояние Махаланобиса от объекта до центра его группы значительно выше, чем от него до центра других групп, а апостериорная вероятность попадания в свою группу ниже критического значения. В этом случае объект считается некорректно отнесенным и должен быть исключён из выборки. Процедура исключения объекта из обучающих выборок состоит в том, что в таблице исходных данных у объекта, который должен быть исключён из выборки (он помечен звездочкой), убирается номер принадлежности к этой группе, после чего процесс тестирования повторяется. По предположению, сначала убирается тот объект, который наиболее не подходит к определённой группе, т.е. у которого наибольшее расстояние Махаланобиса и наименьшая апостериорная вероятность. При удалении очередного объекта из группы нужно помнить, что при этом смещается центр тяжести группы (вектор средних), так как он определяется по оставшимся наблюдениям. После удаления очередного предприятия из списка обучающих выборок не исключено, что появятся новые некорректно отнесенные предприятия, которые до удаления были учтены как правильно отнесённые. Поэтому данную процедуру нужно проводить, удаляя на каждом шаге лишь по одному объекту и возвращая его обратно в обучающие выборки. Если при удаления этого объекта произошли слишком сильные изменения, необходимо вернуться к предыдущему состоянию. Процедура исключения наблюдений продолжается до тех пор, пока общий процент корректности в классификационной матрице достигнет 100 %, т.е. все наблюдения будут правильно отнесены к соответствующим группам. 5. На основе полученных обучающих выборок можно проводить повторную классификацию тех объектов, которые не попали в обучающие выборки, и любых других объектов, подлежащих группировке. Для решения данной задачи существуют два варианта: первый – провести классификацию на основе дискриминантных функций, второй – на основе классификационных функций. В первом случае необходимо, не закрывая диалогового окна Discriminant Function Analisis Results, добавить в таблицу исходных скорректированных данных новые наблюдения. Для того чтобы понять, к какому классу относится этот объект, нажмите кнопку (рис. 2) Posterior probabilities (Апостериорные вероятности). Появится таблица с апостериорными вероятностями. К тем классам, которые будут иметь максимальные вероятности, можно отнести новые наблюдения. Во втором варианте необходимо в диалоговом окне Discriminant Function Analisis Results (рис. 2) нажать кнопку Classification functions. Появится окно, из которого можно выписать дискриминантные функции для каждого класса (рис. 4). Например, для первых двух классов функции имеют вид: Ф1=?78,7186?0,0012*Var1+0,2674*Var2+0,1772*Var3?2,4762*Var4+0,0558*Var5 Интерпретация и использование дискриминантных функций С помощью дискриминантных функций можно будет в дальнейшем классифицировать новые наблюдения. Новые наблюдения будут относиться к тому классу, для которого классифицированное значение будет максимальным. Выбор метода окончательной классификации зависит от количества новых объектов, подлежащих классификации. Если количество новых наблюдений невелико, можно применить метод, основанный на статистических критериях. Если же количество новых наблюдений велико, то рациональнее по обучающим выборкам получить классификационные функции, получить формулы и провести окончательную классификацию. На рис. изображены регрессионные модели для первых двух классов. Для построения графиков значения функций Ф1 и Ф2 рассчитаны по формулам и записаны в переменные Var 6 и Var 7 соответственно. Затем в модуле Statistics/ Scatterplots построены графики рассеяния Var 6 и Var 7 от переменных Var 2 и Var 5 (можно выбрать и остальные переменные). Как видим, классы 1 и 2 хорошо различаются. Дискриминантные функции могут быть также интерпретированы обычным образом: чем больше стандартизованный коэффициент, тем больше вклад соответствующей переменной в дискриминацию совокупностей. Но эти коэффициенты не дают информации о том, между какими совокупностями дискриминируют соответствующие функции. Можно определить характер дискриминации для каждой дискриминантной (канонической) функции, взглянув на средние значения функций для всех совокупностей. Также можно посмотреть, как две функции дискриминируют между группами, построив значения, которые принимают обе дискриминантные функции (рис. 5). Значимость дискриминантной функции Можно проверить коэффициенты, которые значимо добавляется к дискриминации между совокупностями. Для интерпретации могут быть использованы только те из них, которые будут признаны статистически значимыми. Остальные должны быть проигнорированы. Малое значение коэффициента говорит о том, что отдельного класса для дискриминируемых объектов создавать не следовало Для примера на рис. 11.6 приведена функция Ф2, она же без коэффициента при Var1 (0,0021) и Ф2 без коэффициента при Var5 (0,0011). Из регрессионных моделей видно, что коэффициент 0,0021 значим (графики сильно отличаются), а 0,0011 нет. Зрительная проверка не всегда хороша, но можно использовать средние значения. Как и в регрессионном анализе, малые отклонения не существенны, однако прежде чем сделать окончательные выводы при важных исследованиях, неплохо обратить внимание на внутригрупповые матрицы дисперсий и корреляций. В частности, можно построить матричную диаграмму рассеяния, весьма полезную для этой цели. При наличии сомнений можно попробовать произвести анализ заново, исключив одну или две малоинтересных совокупности. Если общий результат сохраняется, по-видимому, решение разумно. Результаты дискриминантного анализа Результаты классификации наблюдений можно вывести в терминах расстояний Махаланобиса, апостериорных вероятностей и собственно результатов классификации, а значения дискриминантной функции для отдельных наблюдений можно просмотреть на обзорных пиктографиках и других многомерных диаграммах, доступных непосредственно из таблиц результатов. Все эти данные можно автоматически добавить в текущий файл данных для дальнейшего анализа. Можно вывести также итоговую матрицу классификации, где указано число и процент правильно классифицированных наблюдений. Имеются различные варианты задания априорных вероятностей принадлежности классам, а также условий отбора, позволяющих включать или исключать определенные наблюдения из процедуры классификации (например, чтобы затем проверить её качество на новой выборке). Плохо обусловленные матрицы Переменные, используемые для дискриминации между совокупностями, не являются полностью избыточными. При вычислении результатов дискриминантного анализа происходит обращение матрицы дисперсий и ковариаций для переменных в модели. Если одна из переменных полностью избыточна по отношению к другим переменным, то такая матрица называется плохо обусловленной и не может быть обращена. Например, если переменная является суммой трех других переменных, то это отразится также и в модели, и рассматриваемая матрица будет плохо обусловленной. Результаты
|
Система статистических методов управления –
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a posteriori - исходя из опыта, на основании опыта (лат.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a priori - заранее, независимо от опыта (лат.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если вы знакомы с пошаговой процедурой множественной регрессии, то вы можете интерпретировать значение F для включения-исключения в том же самом смысле, что и в пошаговой регрессии |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В данном примере в качестве группирующей переменной выбрана Class, а в качестве независимых – все остальные |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
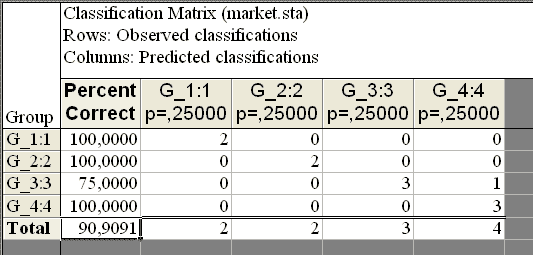
Матрица классификации содержит число образцов, корректно классифицированных (на диагонали матрицы) и тех, которые попали не в свои группы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В этих классах процент корректности равен 100 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Здесь этот процент меньше (75) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расстояние Махаланобиса является мерой расстояния между двумя точками в пространстве, определяемым двумя или более коррелированными переменными. О видах расстояний можно прочитать в книге |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
«Маркетинг и PR практически полностью заменили в нашей стране науку и ремесло в информационных технологиях, а наличие больших денег позволило поначалу закрыть на это глаза, а потом и ослепнуть». Оганесян А. Хаос как предчуствие // CNews. 2006. N6, с.11
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Так решается задача прогноза в промышленной статистике. Например, если показатели качества продукции сильно зависят от исходных материалов, можно предсказать, каков будет конечный результат |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Здесь регрессионные прямые построены для дискриминантных моделей. Надеемся, читатель понимает разницу межлу ними |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коэффициенты дискриминантной функции отражают частный вклад каждой переменной в отдельную дискриминантную функцию
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Малое значение коэффициента говорит о том, что отдельного класса для дискриминируемых объектов создавать не следовало |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
О плохо обусловленных матрицах рассказано в разделе |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Система статистических методов управления – |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Желаете участвовать в семинаре? Хотите написать? Электронная почта - tomsk@ieee.org (Стукач Олег Владимирович) |