Регрессия, корреляция и совпадение

Зависимость

Основная задача регрессионного и корреляционного анализа состоит в выявлении связи между случайными переменными. Например, на свободном рынке обычно наблюдается большая степень корреляции между размером урожая и рыночными ценами на соответствующую продукцию сельского хозяйства. Часто корреляция привлекает наше внимание к причинно-следственным связям, существующим между изучаемыми двумя рядами величин. В области естественных и общественных наук установление существенной корреляции часто заставляет нас искать возможные связи между явлениями, которые в противном случае могли остаться незамеченными.

В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует не какое-то определённое, а множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определённое условное распределение другой переменной. Такая зависимость получила название статистической.

Возникновение понятия статистической связи обусловливается тем, что зависимая переменная подвержена влиянию неконтролируемых или неучтённых факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.

Статистическая зависимость между двумя переменными, при которой каждому значению одной переменной соответствует определённое условное математическое ожидание (среднее значение) другой, называется корреляционной.

Функциональная зависимость представляет собой частный случай корреляционной. При функциональной зависимости с изменением значений некоторой переменной xоднозначно изменяется определенное значение переменной y, при корреляционной – определённое среднее значение (математическое ожидание) y, а при статистической – определённое распределение переменной y. Каждая корреляционная зависимость является статистической, но не каждая статистическая зависимость является корреляционной.  

Статистические связи между переменными можно изучать методами корреляционного и регрессионного анализа. Основной задачей корреляционного анализа является выявление связи между случайными переменными и оценка её степени. Основной  задачей регрессионного анализа является установление формы и изучение зависимости между переменными.

Корреляция

Корреляция определяет степень, с которой значения двух переменных «пропорциональны» друг другу. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость «можно представить» прямой линией (с положительным или отрицательным углом наклона). Таким образом, это простейшая регрессионная модель, описывающая зависимость одной переменной от одного фактора.

В производственных условиях обычно информации, полученной из диаграмм рассеяния при условии их корректного построения, бывает достаточно для того, чтобы оценить степень зависимости у от х. Но в ряде случаев требуется дать количественную оценку степени связи между величинамих и у. Такой оценкой является коэффициент корреляции.

Отметим основные характеристики этого показателя.

• Он может принимать значения от –1 до +1. Знак «+» означает, что связь прямая (когда значения одной переменной возрастают, значения другой переменной также возрастают), «–» означает, что связь обратная.
• Чем ближе коэффициент к |1|, тем теснее линейная связь. При величине коэффициента корреляции менее 0,3 связь оценивается как слабая, от 0,31 до 0,5 – умеренная, от 0,51 до 0,7 – значительная, от 0,71 до 0,9 – тесная, 0,91 и выше – очень тесная.
• Если все значения переменных увеличить (уменьшить) на од­но и то же число или в одно и то же число раз, то величина коэф­фициента корреляции не изменится.
• При r=±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на общей прямой. Её ещё называют линией регрессии.
• При r=0 линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общи­ми средними, а линии регрессии параллельны осям координат.

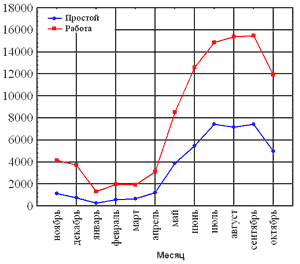
Равенство r=0 говорит лишь об отсутствии линейной корреляционной зависимости (некоррелирован­ности переменных), но не вообще об отсутствии корреляционной, а тем более, статистической зависимости.

Основываясь на коэффициентах корреляции, вы не можете строго доказать причинной зависимости между переменными, однако можете определить ложные корреляции, т.е. корреляции, которые обусловлены влияниями «других», остающихся вне вашего поля зрения переменных. Лучше всего понять ложные корреляции на простом примере. Известно, что существует корреляция между ущербом, причиненным пожаром, и числом пожарных, тушивших пожар. Однако эта корреляция ничего не говорит о том, насколько уменьшатся потери, если будет вызвано меньше число пожарных. Причина в том, что имеется третья переменная (начальный размер пожара), которая влияет как на причинённый ущерб, так и на число вызванных пожарных. Если вы будете учитывать эту переменную, например, рассматривать только пожары определённой величины, то исходная корреляция между ущербом и числом пожарных либо исчезнет, либо, возможно, даже изменит свой знак. Основная проблема ложной корреляции состоит в том, что вы не знаете, кто является её носителем. Тем не менее, если вы знаете, где искать, то можно воспользоваться частные корреляции, чтобы контролировать (частично исключённое) влияние определённых переменных.

Корреляция, совпадение или необычное явление сами по себе ничего не доказывают, но они могут привлечь внимание к отдельным вопросам и привести к дополнительному исследованию. Хотя корреляция прямо не указывает на причинную связь, она может служить ключом к разгадке причин. При благоприятных условиях на её основе можно сформулировать гипотезы, проверяемые экспериментально, когда возможен контроль других влияний, помимо тех немногочисленных, которые подлежат исследованию.

Иногда вывод об отсутствии корреляции важнее наличия сильной корреляции. Нулевая корреляция двух переменных может свидетельствовать о том, что никакого влияния одной переменной на другую не существует, при условии, что мы доверяем результатам измерений.

Корреляционный анализ в программе Statistica

Корреляционный анализ в программе Statistica проводят с помощью модуля Statistics/ BasicStatistics/ CorrelationMatrices. В стартовом окне этой процедуры для расчёта квадратной матрицы используется кнопка Onevariablelist. С помощью кнопки Twolists (rect. matrix) можно ограничиться выводом только необходимых переменных, если не требуются все возможные парные корреляции. В списке переменных выбирают переменные, между которыми будут рассчитаны парные коэффициенты корреляции Пирсона. После нажатия на кнопку Summary или Correlations на экране появится корреляционная матрица.

Процедура Correlationmatricesсразу же дает возможность проверить достоверность рассчитанных коэффициентов корреляции. Значение коэффициента корреляции может быть высоким, но не достоверным, случайным. Чтобы увидеть вероятность нулевой гипотезы (p), гласящей о том, что коэффициент корреляции равен нулю, нужно в опции Displayformatforcorrelationmatricesустановить переключатель на вторую строку Displayr, p-levels, andN’s. Но даже если этого не делать и оставить переключатель в первом положении Displaysimplematrix (highlightp’s), статистически значимые на уровне 0,05 коэффициенты корреляции будут выделены в корреляционной матрице на экране красным цветом, а при распечатке помечены звездочкой. Третье положение переключателя опции DisplayDetailedtableofresultsпозволяет просмотреть результаты корреляционного анализа в деталях. Флажок опции MDdeletionустанавливается для исключения из обработки всей строки файла данных, в которой есть хотя бы одно пропущенное значение.

Для построения диаграмм рассеяния необходимо во вкладке Quickстартового модуля Statistics/ BasicStatistics/ CorrelationMatricesнажать кнопку Scatterplotmatrixforselectedvariables. В результате этих действий появится графическое изображение зависимостей. Остаётся только посмотреть на полученный результат и сделать выводы.

Проведённая прямая в каждой диаграмме рассеяния называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси ординат) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.
По главной диагонали матрицы строятся гистограммы. Понятно, что любая переменная стопроцентно коррелирует сама с собой, и строить линию регрессии не имеет смысла.

Во многих исследованиях первый шаг анализа состоит в вычислении корреляционной матрицы всех переменных и проверке значимых (ожидаемых и неожиданных) корреляций. После того как это сделано, следует понять общую природу обнаруженной статистической значимости: понять, почему одни коэффициенты корреляции значимы, а другие нет.

Но следует иметь в виду, что если используется несколько критериев, значимые результаты могут появляться «удивительно часто», и это будет происходить чисто случайным образом. Например, коэффициент, значимый на уровне 0,05, будет встречаться чисто случайно один раз в каждом из 20 подвергнутых исследованию коэффициентов. Нет способа автоматически выделить «истинную» корреляцию. Поэтому следует подходить с осторожностью ко всем не предсказанным или заранее не запланированным результатам и попытаться соотнести их с другими (надёжными) результатами. В конечном счете, самый убедительный способ проверки состоит в проведении повторного экспериментального исследования. Такое положение является общим для всех методов анализа, использующих множественные сравнения и статистическую значимость.

Рассмотрим пример решения практической задачи о производительности землеройной техники. Из-за сезонного характера работ неизбежны простои. Но поскольку простой техники обходится дорого, руководство предприятия интересовали пути сокращения простоев, в частности, в летние месяцы. В таблице приведены данные о работе и простое всего парка в машино-часах.

Сначала имеет смысл отобразить данные на графике. Чтобы построить два графика на одной сетке, необходимо выбрать модуль Graphs/ Scatterplots…После чего появится диалоговое окно, в котором необходимо выбрать вкладку Advanced. Далее следует выбрать необходимые переменные и тип графика. После нажатия на кнопку ОК график будет выведен в отдельном окне на рабочем пространстве системы.

Графики рассеяния и корреляционный анализ показали, что сезонность не является фактором, влияющим на простой. Налицо почти линейная зависимость между работой и простоями, то есть чем больше техника находится в работе, тем дольше она будет простаивать.

Корреляционная матрица для производительности землеройной техники

* – коэффициенты, значимые по уровню 0,05

Понятно, что для решения задачи сокращения простоев техники нужно выявить влияющие факторы и искать статистическую зависимость от них. Этот пример показывает, что степень связи между любыми двумя переменными, независимо от того, как эта связь выражена, зависит от характера измерения переменных.

Ранговая корреляция

На практике часто изучают связи между порядковыми переменными, измеренными в так называемой порядковой шкале. В этой шкале можно установить лишь порядок, в котором объекты выстраиваются по степени проявления признака (например, качество жилищных условий, тестовые баллы, экзаменационные оценки). Если, скажем, по некоторой дисциплине два студента имеют оценки «отлично» и «удовлетворительно», то можно лишь утверждать, что уровень подготовки по этой дисциплине первого студента лучше, чем второго, но нельзя сказать, на сколько.

Оказалось, что в таких случаях проблема оценки тесноты связи разрешима, если упорядочить, или ранжировать объекты анализа по степени выраженности измеряемых признаков. При этом каждому объекту присваивается определённый номер, называемый рангом. Например, объекту с наименьшим проявлением (значением) признака присваивается ранг 1, следующему за ним – 2 и т.д. Объекты можно располагать и в порядке убывания проявления признака.

Ранжируя попарно связанные значения признаков, можно видеть, как они распределяются относительно друг друга. Если возрастающим значениям одного признака соответствуют возрастающие значения другого, то между ними существует положительная связь. Если же при возрастании значений одного признака значения другого последовательно уменьшаются, это указывает на наличие отрицательной связи между ними. При отсутствии корреляции ранжированным значениям одного признака будут соответствовать самые различные значения другого.

Определив ранги значений переменных, по коэффициенту ранговой корреляции Спирмена можно судить о степени зависимости одного признака от изменений другого.

Для примера рассмотрим вычисление ранговой корреляции между рейтингом подразделения и премиальным фондом

Выберите модуль Statistics/ Nonparametrics, в появившемся стартовом окне выберите пункт Correlations (Spearman Kendall tau, gamma) / кнопка ОК. В открывшемся диалоговом окне выберите исследуемые признаки кнопкой Variables (List 1 – Var 1, List 2 – Var 2). После нажатия на кнопку SpearmanrankRполучим окно с результатами корреляционного анализа.

Spearman Rank Order Correlations
MD pairwise deleted
Marked correlations are significant at p<,05000

Коэффициент корреляции Спирмена равен 0,618 с уровнем p-level 0,10. Это означает, что связь рейтинга, выражающего результативность работы, и премиального фонда статистически незначима по уровню 0,05.

В пакете Statistica коэффициент ранговой корреляции Кендалла вычисляется в процедуре Statistics/ Nonparametrics, в появившемся стартовом окне выберите пункт Correlations (Spearman Kendall tau, gamma) / кнопка ОК. В открывшемся диалоговом окне выберите исследуемые признаки кнопкой Variables (List 1 – Var 1, List 2 – Var 2). После нажатия на кнопку Kendall Tau во вкладке Advancedполучим окно с результатами корреляционного анализа.

Kendall Tau Correlations
MD pairwise deleted
Marked correlations are significant at p<,05000

Выборочное значение tau=0,416, то на уровне значимости alpha=0,05, что меньше p, ранговая корреляция незначима. Так как квантиль распределения N(0, 1) u0,95=1,645, что больше выборочного значения Z, коэффициент ранговой корреляции t незначимо отличается от нуля. Это означает, что связь рейтинга, выражающего результативность работы, и премиального фонда статистически незначима по уровню 0,05.

Рассмотренные примеры отличаются малым числом наблюдений. Для надёжного результата общее число наблюдений не должно быть меньше 50. Несоблюдение этого требования не гарантирует достаточно точных выводов, которые делают на основании выборочных показателей.

Регрессионный анализ

Регрессионный анализ является одним  из наиболее распространённых методов обработки экспериментальных данных при изучении зависимостей в физике, биологии, экономике, технике и других областях.

Исследование объективно существующих связей между явлениями – важнейшая задача общей теории статистики. Регрессионный анализ заключается в определении аналитического выражения, в котором изменение одной величины (называемой зависимой или результативным признаком) y обусловлено  влиянием одной или нескольких независимых величин (факторов) x1, x2,…, xn, а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения.

Регрессия может быть однофакторной (парной) и многофакторной (множественной). Для простой (парной) регрессии в условиях, когда достаточно полно установлены причинно-следственные связи, можно использовать графическое изображение. При множественности причинных связей невозможно чётко разграничить одни причинные явления от других. В этом случае наиболее приемлемым способом определения зависимости (уравнения регрессии) является метод перебора различных уравнений, реализуемый с помощью компьютера.

После выбора вида регрессионной модели, используя результаты наблюдений зависимой переменной и факторов, нужно вычислить оценки (приближённые значения) параметров регрессии, а затем проверить значимость и адекватность модели результатам наблюдений.

Порядок проведения регрессионного анализа следующий:

• выбор модели регрессии, что заключает в себе предположение о зависимости функций регрессии от факторов;
• оценка параметров регрессии в выбранной модели методом наименьших квадратов;
• проверка статистических гипотез о регрессии.

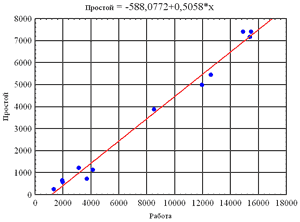
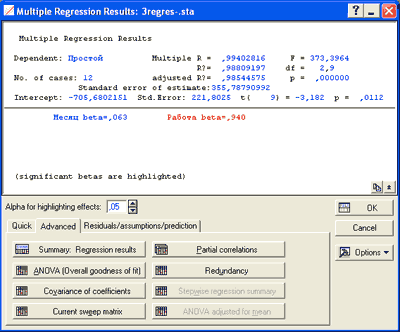
Пример проведения регрессионного анализа данных

Построим приближённую зависимость времени простоя техники от времени работы и месяца. На существование этой зависимости, причём линейной, указывает корреляционный анализ. Имея зависимость, выраженную в виде формулы, можно прогнозировать время простоя на следующий период и оценить недополученную прибыль в результате простоев, что так любят делать экономисты.

Линейный регрессионный анализ выполняется в модуле Statistics/ MultipleRegression. В стартовом диалоговом окне этого модуля при помощи кнопки Variables указываются зависимая (dependent) и независимые (independent) переменные. В поле Inputfileуказывается тип файла с данными:
RawData – данные в виде строчной таблицы (по умолчанию);
CorrelationMatrix – данные в виде корреляционной матрицы.

В стартовом окне можно задать и дополнительные опции и параметры анализа. Например, можно выбрать определенное подмножество наблюдений для анализа или приписать вес переменным. Также можно задать и опции, которые относятся непосредственно к статистической процедуре: задать правило обработки пропущенных данных, выбрать метод анализа по умолчанию и др.

Для вывода результатов и их анализа нажмите на кнопку ОК.  Система произведет вычисления, и на экране появитсяокно результатов. Оно имеет простую структуру: верхняя часть окна – информационная, нижняя содержит функциональные кнопки, позволяющие всесторонне просмотреть результаты анализа.

Dependent  – имя зависимой переменной. В нашем случае это «Простой».

No. of cases –  число наблюдений, по которым построена регрессия. В примере число равно 12.

Multiple R – коэффициент множественной корреляции. Эта статистика полезна в множественной регрессии, когда вы хотите описать зависимости между переменными. Она может принимать значения от 0 до 1 и характеризует тесноту линейной связи между зависимой и всеми независимыми переменными.

R? – квадрат коэффициента множественной корреляции (R2), называемый коэффициентом детерминации.

Коэффициент детерминации является одной из основных статистик в данном окне, он  показывает долю общего разброса (относительно выборочного среднего зависимой переменной), которая объясняется построенной регрессией. Чем ближе коэффициент детерминации к единице, тем качественнее найдена модель (объясняет поведение большего числа точек).

Коэффициент детерминации обладает существенным недостатком. При равенстве числа независимых переменных q числу наблюдений n величина R2 равна 1. По мере добавления переменных в уравнение значение R2 неизбежно возрастает. Это ведет к неоправданному предпочтению моделей с большим числом независимых переменных. Отсюда следует, что необходима поправка к R2, которая бы учитывала число переменных и наблюдений. В результате получаем скорректированный коэффициент детерминации (adjusted R?).

Включение новой переменной в регрессионное уравнение увеличивает R2 не всегда, а только в том случае, когда частный F-критерий при проверке гипотезы о значимости включаемой переменной больше или равен 1. В противном случае включение новой переменной уменьшает значение коэффициентов детерминации. Таким образом, скорректированный R2 можно с большим успехом (по сравнению с R2) применять для выбора наилучшего подмножества независимых переменных в регрессионном уравнении.

F-критерий используется для оценки адекватности регрессионной модели, определяет отношение дисперсии оценки модели к дисперсии остатка.

Standard Error of estimate –   стандартная ошибка оценки. Эта статистика является мерой рассеяния наблюдаемых значений относительно регрессионной прямой.

Intercept – оценка свободного члена регрессии. Значение коэффициента b0 в уравнении регрессии.

Std. Error – стандартная ошибка оценки свободного члена. Стандартная ошибка коэффициента b0 в уравнении регрессии.

F – значения F-критерия для проверки гипотезы b1=0.
df – число степеней свободы F-критерия.
p – уровень значимости.
t–t-критерий для проверки гипотезы о равенстве нулю свободного члена уравнения. Если p больше заданного уровня значимости Alpha,  то гипотеза b0=0 принимается.
Beta – коэффициенты b уравнения.

В информационной части прежде всего нужно смотреть на значение коэффициента детерминации. В нашем примере он равен 0,988... Это значит, что построенная регрессия объясняет 98,8 % разброса значений переменной «Простой» относительно среднего. Это хороший результат.

Далее смотрим на значение F-критерия и уровень его значимости p. F-критерий используется для проверки гипотезы, утверждающей, что между зависимой переменной «Простой» и независимой переменной «Работа» нет линейной зависимости, т.е. b1=0, против альтернативы «b1 не равен нулю». В данном примере большое значение F-критерия 373,3964 и даваемый в окне уровень значимости p=0,0112 показывают, что построенная регрессия значима.

При помощи кнопок диалогового окна Multiple Regressions Results результаты регрессионного анализа можно просмотреть более детально. Щёлкните далее на кнопку Summary:Regression rezults (краткие результаты регрессии). 

Во втором столбце таблицы (Beta) выводятся стандартизованные коэффициенты регрессии, в третьем (Std.Err. of Beta) – их стандартные отклонения. В случае множественной регрессии стандартизованные коэффициенты регрессии используются для сравнения влияния на зависимую переменную факторов, имеющих различную размерность.
В четвёртом столбце таблицы имеются оценки неизвестных параметров модели:
b0 = –705,680;
b1 = 51,152;
b2 = 0,479;
в пятом столбце (St.Err. of B) – их стандартные отклонения.
Итак, искомая модель зависимости времени простоя техники от времени работы и месяца имеет вид:
                Простой = –705,680+51,152*Месяц+ 0,479*Работа+?.

Из модели очевидна необходимость снижения сезонности работ.
В шестом и седьмом столбцах таблицы выводятся t-статистики и соответствующие уровни значимости для проверки гипотезы о равенстве нулю коэффициентов регрессии. Для нашего примера гипотеза для b0 и b2 отклоняется.

Оценка адекватности модели по остаткам

Для оценки адекватности модели необходимо исследовать остатки. Остатки – это разность между исходными (наблюдаемыми) значениями зависимой переменной и предсказанными (модельными, Predicted values) значениями. Остатки должны быть нормально распределены, иметь нулевое среднее значение и постоянную дисперсию, независимо от величин зависимых и независимых переменных. Модель должна быть адекватна на всех отрезках интервала изменения зависимой переменной. Вначале для оценки адекватности модели лучше всего использовать визуальные методы и затем, если потребуется, перейти к статистическим критериям.

В большинстве случаев одного графического анализа остатков бывает вполне достаточно

Для исследования остатков в окне результатов регрессионного анализа необходимо выбрать вкладку Residuals/assumptions/prediction и нажать кнопку Perform residual analysis. Для оценки адекватности модели построим нормальный вероятностный график остатков. В отобразившемся окне, перейдя к вкладке Quick, необходимо нажать кнопку Normal plot of residuals.

Если остатки достаточно хорошо ложатся на прямую, которая соответствуют нормальному закону, предположение о нормальном распределении ошибок выполнено.

Для выявления нестабильности дисперсии ошибки уравнения можно построить график зависимости регрессионных остатков от предсказанного значения зависимой переменной. Во вкладке Scatterplots нажмите кнопку Predictedvs. residuals. В результате будет построен график. Из этого графика видно, что остатки хаотично разбросаны относительно прямой, в их поведении нет закономерностей. Нет оснований говорить, что остатки связаны между собой, нет также резко выделяющихся остатков. Отсюда можно заключить, что модель достаточно адекватно описывает данные.

Читать дальше