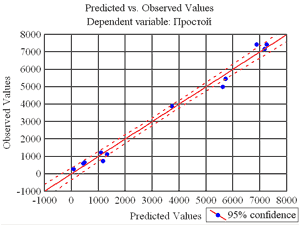
Регрессия, корреляция и совпадение

Начало

Очень удобным визуальным способом оценки адекватности регрессионной модели является анализ графика опытных и полученных по регрессионному уравнению  значений зависимой переменной. Он строится при помощи кнопки Predictedvs. observedокна анализа остатков.

Хорошо видно, что линейный вид модели хорошо описывает взаимосвязь переменной «Простой» от месяца и времени работы. Эта связь носит линейный характер. Важно просмотреть графики зависимости остатков от каждой из независимых переменных. Эти графики полезны для обнаружения нелинейной зависимости от переменных. Их легко просмотреть при помощи кнопки Residualsvs. independentvar. вкладки Residuals. Остатки должны быть нормально распределены, т.е. на графике они должны представлять приблизительно горизонтальную полосу одинаковой ширины на всем ее протяжении. Коэффициент корреляции между регрессионными остатками и переменными должен равняться нулю. Присутствие нелинейного тренда в регрессионных остатках вызывает сомнение в адекватности модели и говорит о необходимости пересмотра модели – преобразования или ввода новых переменных, перехода к нелинейной модели. Может, например, оказаться, что в исходную модель нужно включить в слагаемое x₂ или перейти от x к logx. Линейная модель регрессии предполагает, что переменные не взаимодействуют друг с другом, и изменение одного из них не оказывает никакого влияния на значения других. Чтобы проверить справедливость этого предположения, нужно построить график остатков от произведения x₁x₂. Если график имеет вид линейного тренда, то в модель нужно ввести x₁x₂.

Следует заметить, что мы имеем очень небольшое число данных – всего 12. Поэтому мы используем графические методы оценки адекватности модели. В сложных задачах графические и статистические методы оценки адекватности должны естественно дополнять друг друга.

Кнопка Redundancy предназначена  для поиска выбросов. Выбросы – это остатки, которые значительно превосходят по абсолютной величине остальные. Выбросы дают данные, которые являются не типичными по отношению к остальным данным и требуют выяснения причин их возникновения. Выбросы должны исключаться из обработки, если они вызваны ошибками измерения. Для выделения выбросов, имеющихся в регрессионных остатках, предложены следующие метрики:

Расстояние Р.Д. Кука (Cook's Distance) показывает расстояние между коэффициентами уравнения регрессии после исключения из обработки каждой точки данных. Большое значение показателя Кука указывает на сильно влияющее наблюдение.
Расстояние Махаланобиса (Mahalanobis Distance) показывает, насколько каждое наблюдение отклоняется от центра статистической совокупности.

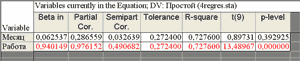
Корреляционный и дисперсионный анализ модели

Частная корреляция – это корреляция между двумя переменными, когда одна или больше из оставшихся переменных удерживаются на постоянном уровне. Частные коэффициенты корреляции, как и парные, могут принимать значения от –1 до +1. Кнопка Partialcorrelations окна результатов регрессионного анализа позволяет просмотреть частные коэффициенты корреляции (Partial Cor.) между переменными.

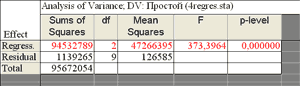
В идеальной регрессионной модели независимые переменные вообще не коррелируют друг с другом. В самом деле, если две независимые переменные сильно коррелированы с откликом и друг с другом, то достаточно включить в уравнение только одну из них. Обычно включают ту переменную, значения которой легче и дешевле измерять.

Сильная взаимная коррелированность независимых переменных в нашем уравнении затрудняет анализ влияния отдельных факторов на зависимую переменную. Сильная коррелированность переменных в моделях, разрабатываемых для промышленных приложений, является частым явлением. Это приводит к увеличению ошибок уравнения, уменьшению точности оценивания. Общая эффективность использования регрессионной модели снижается. Поэтому выбор независимых переменных, включаемых в регрессионную модель, необходимо проводить очень тщательно.

Кнопка ANOVA (Overallgoodnessoffit) окна результатов регрессионного анализа позволяет ознакомиться с результатами дисперсионного анализа уравнения регрессии.

В строках таблицы дисперсионного анализа уравнения регрессии записаны источники вариации: Regress. – обусловленная регрессией, Residual – остаточная, Total – общая. Значения столбцов таблицы: Sums of Squares – сумма квадратов, df – число степеней свободы, Mean Squares – среднеквадратическое значение, F – значение F-критерия, p-level – вероятность нулевой гипотезы для F-критерия. Видим, что F-критерий полученного уравнения регрессии значим на 0,05-уровне. Вероятность нулевой гипотезы (p-level) значительно меньше 0,05, что говорит об общей значимости уравнения регрессии.

Кнопка Predictdependentvariableпозволяет рассчитать по полученному регрессионному уравнению значение зависимой переменной по значениям независимых переменных, которые необходимо ввести в появляющемся диалоговом окне.

Кнопка Descriptivestatisticsпозволяет просмотреть описательные статистики и корреляционную матрицу с парными коэффициентами корреляции переменных, участвующих в регрессионной модели.

Фиксированная нелинейная регрессия

В некоторых случаях нелинейные модели с помощью специальных линеаризирующих преобразований могут быть преобразованы в линейные. Рассмотрим порядок нахождения коэффициентов уравнений нелинейной регрессии, которые через преобразования переменных могут быть приведены к линейной модели. В качестве примера рассмотрим экономические показатели некоторого предприятия за три квартала текущего года. Предположим, что необходимо определить, как влияют на полученную прибыль (y) доходы (x₁), фонд оплаты труда рабочих (x₂) и накладные расходы (x₃). Полученная формула, например, позволит составить прогноз на следующий месяц и оценить значимость каждого фактора.

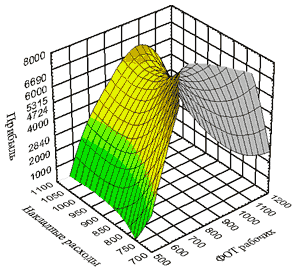
В качестве метода разведочного анализа выберем построение трёхмерных графиков. Видно, что зависимость переменной y от x₁, x₂ и x₃ явно нелинейная.

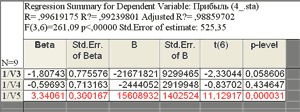
Следовательно, можно попытаться найти модель в виде: y=b₁/x₁+b₂/x₂+b₃/x₃+ε.

После запуска модуля фиксированной регрессии Statistics/AdvancedLinear/NonlinearModels/ FixedNonlinearRegression и выбора переменных после нажатия на кнопку ОК в диалоговом окне Non-linearComponentsRegression можно выбрать типы преобразования переменных в виде широко распространённых математических функций. Для нашего примера это 1/x. Если потребуются какие либо иные преобразования переменных, то эти преобразования нужно делать в таблице с исходными данными, а затем включить полученные фиктивные переменные в качестве зависимых в регрессионную модель.

После того, как тип преобразования переменных определён, необходимо уточнение зависимой и независимых переменных фиксированной нелинейной регрессионной модели. Оно производится на следующем шаге при помощи кнопки Variables диалогового окна «Уточнение модели» – ModelDefinition. В этом окне установим значение поля Intercept на «Set to zero», что позволит получить регрессионную модель без свободного члена уравнения, то есть b₀=0.

Зависимой переменной (Dependent variables)  в нашем случае будет «Прибыль» y; независимыми (Independent variables) – обратные величины 3, 4 и 5 переменной по списку, то есть 1/x₁, 1/x₂ и 1/x₃.

Результаты появляются при нажатии кнопки OK.

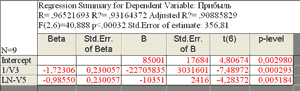
Уравнение с найденными коэффициентами имеет вид:

y=-21671821,4/x₁-2444052,3/x₂+15608932,1/x₃+ε.

Все коэффициенты уравнения значимы по уровню 0,05. Уравнение объясняет 99,24 % (R2 = 0,9924) вариации зависимой переменной. По анализу остатков можно убедиться в адекватности полученной модели. Ошибка уравнения составляет 525,35. Если сравнить абсолютную величину ошибки со средним значением зависимой переменной: 525,35/4791,8527*100 %=10,96 %, то заметим, что она довольно велика. Следовательно, модель нуждается в совершенствовании.

Пошаговая регрессия

Поиск наилучшей регрессионной модели – это сложный и громоздкий процесс. При помощи опции Method пользователь может отказаться от стандартного проведения регрессионного анализа (Standard) и воспользоваться методами пошагового включения переменных в регрессионную модель (Forwardstepwise) или пошагового исключения переменных (Backwardstepwise) из регрессионной модели. Эти методы можно использовать в сложных системах с большим числом переменных. Опция Displaying results вкладки Stepwise позволяет просматривать итоговые результаты регрессионного анализа (Summary only) или после каждого шага включения или исключения переменных (At each step).

Воспользуемся методом пошагового включения переменных для нахождения наилучшего регрессионного уравнения для предыдущих данных. В качестве независимых переменных, которые потенциально могут быть включены в модель для y примем переменные x₁, x₂, x₃, их обратные значения 1/x₁, 1/x₂, 1/x₃ и натуральные логарифмы ln(x₁), ln(x₂), ln(x₃).

Для пошаговых методов можно установить величину Tolerance (допуск) и величины частного F-критерия для включения в модель (Ftoenter) и исключения из неё (Ftoremove). Величина допуска является границей для включения в модель переменных, допуск на которые меньше установленного. Если величина допуска мала, то переменная несёт малую дополнительную информацию, она незначима и включение её в модель не целесообразно. Характерно, что новая независимая переменная, включаемая в модель, может сильно повлиять на зависимую переменную. Наоборот, если она включается в модель после других переменных, она может уже мало влиять на зависимую переменную, например, из-за сильной коррелированности с переменными, уже включёнными в модель. По умолчанию в пакете Statistica переменная включается в модель, если частный F-критерий больше или равен 1. Численное значение F-критерия для включения никогда не выбирается меньшим, чем численное значение F-критерия для исключения. Воспользуемся установками по умолчанию и запустим анализ. В результате процедуры пошагового включения переменных в регрессионную модель получено следующее уравнение: y=850001,1-22705835,2/x₁-10350,98*ln(x₃)+ε.

Видно, что все коэффициенты уравнения значимы по уровню 0,05 (p-level<0,05). Это уравнение объясняет 93,16 % (R2=0,9316) вариации зависимой переменной. Средняя ошибка составляет 356,81, что почти в 1,5 раза меньше, чем в предыдущей модели. Итак, согласно полученной ранее модели, прибыль тем больше, чем больше фонд оплаты труда. В уточнённой модели, прибыль зависит от дохода и накладных расходов, но не зависит от фонда оплаты труда. Компьютер исключил как незначимую эту переменную, поступив куда умнее руководителя предприятия, вечно экономящего на зарплате.

Наилучшие регрессионные модели

Технические навыки при работе в системе Statistica – это ремесло, которому может научиться каждый. Поиск наилучшей регрессионной модели – это искусство, у которого нет рецептов. С одной стороны, для получения надёжных прогнозов значений отклика y в модель нужно включать как можно больше независимых переменных. С другой стороны, с увеличением их числа возрастает дисперсия прогноза и увеличиваются затраты, связанные с получением информации о дополнительных переменных, поэтому желательно включать в уравнение как можно меньше переменных. Тем не менее, существуют некоторые общие требования к регрессионным моделям:

• Регрессионная модель должна объяснять не менее 80 % вариации зависимой переменной, т.е. R2>0,8.
• Чем меньше сумма квадратов остатков, чем меньше стандартная ошибка оценки и чем больше R2, тем лучше уравнение регрессии.
• Коэффициенты уравнения регрессии и его свободный член должны быть значимы по уровню 0,05.
• Стандартная ошибка оценки зависимой переменной по уравнению должна составлять не более 5 % среднего значения зависимой переменной.
• Остатки от регрессии должны быть без заметной автокорреляции (r<0,3), нормально распределены и без систематической составляющей.

Отметим, что понятие «наилучшая регрессионная модель» является субъективным, так как нет никакой единой статистической процедуры для выбора соответствующего подмножества независимых переменных.

Гребневая регрессия

В основе рассмотренного ранее регрессионного анализа лежит метод наименьших квадратов. Его недостатком является относительно небольшая устойчивость к изменениям входных данных. В настоящее время широко стали применяться альтернативные регрессионные модели, одной из которых является гребневая регрессия, которая отличается устойчивостью для случаев сильной коррелированности зависимых переменных друг с другом. В отличие от метода наименьших квадратов, дающего несмещённые оценки коэффициентов уравнения, в методе гребневой регрессии оценки смещённые, но при этом они имеют меньшую дисперсию. Поэтому такие оценки могут давать более точные и приемлемые для практического использования модели.

Для расчёта коэффициентов уравнения гребневой регрессии следует отметить чекбокс в опции Ridgeregression диалогового окна ModelDefinition. При практическом использовании метода гребневой регрессии одним из основных вопросов является выбор параметра λ (lambda). Существуют численные методы расчёта этого параметра, но чаще используют простой опытный подход: начинают расчёт при λ=0, увеличивают параметр с малым шагом, например, 0,001 и следят за ошибкой регрессии и коэффициентами уравнения. Ошибка не должна увеличиваться, а коэффициенты должны стабилизироваться и при дальнейшем увеличении параметра мало изменяться. Значение принятого параметра λ является мерой смещения оценок от истинного значения, поэтому стараются не придавать λ слишком больших значений. Обычно λ выбирают меньше 0,5.